DM15 USER MANUAL
SwissMicros GmbH Copyright © 2016 – 2025 • 2025-10-01
1. Introduction
1.1. Family Members
The Voyager Series of calculators were introduced by Hewlett-Packard in 1981. Each model provided different capabilities and was aimed at different user markets.
The SwissMicros' Series of the Voyager calculators come in two sizes. See the Illustrations section for a visual size comparison. The credit card sized models (e.g. DM15) and the original sized models (e.g. DM15L) contain the same electronics and use the same firmware.
In this document, all models are referenced without trailing L.
-
DM10 — basic scientific calculator
-
DM11 — mid-range scientific calculator
-
DM12 — business/financial calculator
-
DM15 — advanced scientific calculator
-
DM16 — computer programmer’s calculator
-
DM41 — a landscape orientated clone of the HP-41CX
1.2. SwissMicros improvements on the Voyager Series
-
They do not have all the bugs found in the HP-15C LE, see the bug list!
-
They run up to 30 times faster (at 48MHz) than the calculators introduced in the 80s.
-
The USB connection features a command line interface for saving and restoring complete calculator states.
-
Save, edit and restore complete calculator states with one of SwissMicros' online utility.
-
Firmware update via USB is possible using the SwissMicros Firmware Update Tool (on Windows) or standard
lpc21isputility on Linux and MacOS. -
The reset button is located on the back in the lower left-hand side closest to the corner.
-
They are still being produced
1.3. References and Resources
-
Encode and decode utility (html with jscript) for Save and Restore State function
-
Torsten Manz' excellent HP-15C Simulator supports data exchange with the DM15 under Windows, Linux and Mac OS X
2. Fundamentals
This part of the manual covers the basic functions of the DM15 and how to use them. This includes information about getting started, numeric functions, the automatic memory stack, data storage, and statistics functions.
2.1. Getting Started
This section provides the essential information to start operating your DM15 calculator effectively. It covers basic functionalities such as powering on/off and understanding the keyboard layout with its diverse functions.
2.1.1. Powering On and Off
Turning your DM15 on and off is straightforward – simply press the [ON] key. Remember, this calculator is designed with energy efficiency in mind; it will automatically power down after a period of inactivity to conserve battery life.
2.1.2. Understanding the Keyboard
The keyboard layout of the DM15 is designed for efficient access to its diverse range of functions. Let’s explore the different types of functions available:
2.1.2.1. Primary and Alternate Functions
Each key on the DM15 offers three distinct functionalities: a primary function and two alternate functions.
-
Primary Function: This is the function indicated by the label printed directly on the key. For instance, pressing the [÷] key performs division, its primary function.
-
Alternate Functions: These functions are labelled in gold and blue above and below the key, respectively. To access these functions, first press the corresponding gold [f] or blue [g] prefix key, then press the desired function key. For example, to access the square root function labelled in gold above the [×] key, press [f][×].
Note: Throughout this manual, references to alternate functions will follow a specific format. The function itself will be referred to by the key name within a box (e.g., "the [Σ+] function"). When instructing on using the key, the prefix key will be included (e.g., "press [g][Σ+]").
Additional Notes:
-
Pressing the [f] or [g] prefix key will display an "f" or "g" indicator on the screen. This indicator remains until a function key is pressed to complete the operation.
-
If you mistakenly press the wrong prefix key, use [f][CLx] to cancel the error. This action will momentarily display the full mantissa (all digits) of the currently displayed number.
-
The [ON] key is strategically positioned lower than the other keys to prevent accidental presses.
2.1.3. Prefix Keys
Certain functions on the DM15 require a two-part input: a prefix key followed by a digit or another key. Here’s a list of the prefix keys for your reference:
[L.R.] [Σ+] [STO] [RCL] [f] [g]
2.1.4. Changing Signs
To change the sign (positive or negative) of the displayed number, press the [CHS] (change sign) key. When entering a negative number, simply press [CHS] after entering the digits.
2.1.5. Entering Exponents
To input a number with an exponent, use the [EEX] (enter exponent) key. First, enter the mantissa (the significant digits of the number), then press [EEX], and finally, enter the exponent. For a negative exponent, press [CHS] after entering the exponent value.
Example: To enter Avogadro’s number (6.022 × 10²³) and multiply it by 2:
-
Enter: 6.022
-
Press: [EEX]
-
Enter: 23
-
Press: [ENTER]
-
Enter: 2
-
Press: [×]
-
The result (1.2044 × 10²⁴) is displayed
Note: The [CHS] key can be pressed either before or after entering the exponent, both with the same effect. However, for the mantissa, the digits must be entered before pressing [CHS].
2.1.6. Clearing Values
The DM15 provides various ways to clear values, depending on the desired scope:
-
[CLx]: Clears the displayed value (X register) to zero.
-
[←]: Deletes the last entered digit if digit entry is not yet finalized. Otherwise, it functions the same as [CLx].
-
[f][CLΣ]: Clears the statistics registers, the display, and the memory stack (explained later).
-
[f][CLx]: In normal operation, it resets the program memory position to line 000. During program editing, it clears the entire program memory.
-
[f][CL REG]: Clears all data storage registers.
-
[f][CLx]: This key serves a dual purpose: it clears any prefix from a partially entered function sequence and temporarily displays the full mantissa of the displayed number.
Note: The specific behavior of [CLx] and [←] may differ depending on whether you are in normal operation or program editing mode.
2.1.7. Performing Calculations
2.1.7.1. One-Number Functions
One-number functions operate on the currently displayed number. To use them, simply press the corresponding function key after the number is displayed.
Example:
-
Enter: 45
-
Press: [g][LN] (natural logarithm)
-
The result (3.8067) is displayed
2.1.7.2. Two-Number Functions
Two-number functions require two numbers to be present in the calculator before execution. Arithmetic operations like addition, subtraction, multiplication, and division are examples of two-number functions.
To signal the end of the first number entry and prepare for the second number in a two-number function, press the [ENTER] key. This action separates the two numbers and ensures they are treated as distinct values in the calculation.
The DM15 allows you to perform a series of calculations without the need to repeatedly press the [ENTER] key. Each operation automatically stores the result, which can then be used as an operand in the next calculation.
Example: Calculate (9 + 17 – 4) ÷ 4
-
Enter: 9
-
Press: [ENTER]
-
Enter: 17
-
Press: [+]
-
Enter: 4
-
Press: [-]
-
Enter: 4
-
Press: [÷]
-
The result (5.5) is displayed
Important Points:
-
The [ENTER] key is used only to separate consecutive number entries.
-
The operator key is pressed after both operands are entered.
-
Results of operations can be directly used in subsequent calculations.
-
Entering new digits after an operation initiates a new number entry.
With this basic understanding of the keyboard and calculations, you are ready to explore the diverse numerical functions the DM15 offers. This will be covered in the next section.
2.2. Numeric Functions
This section delves into the various numeric functions available on your DM15 calculator, excluding statistical and advanced functions, which will be covered later. These functions allow you to perform a wide range of mathematical operations with ease.
Important Note: The numeric functions operate identically whether used directly from the keyboard or within a program. Also, remember that these functions automatically finalize any ongoing digit entry, so there’s no need to press [ENTER] before or after using them.
2.2.1. Pi
To input the value of pi (π) with 10-digit precision, press [g][π].
2.2.2. Number Alteration Functions
These functions modify the number currently displayed on the screen (in the X register).
-
[g][INTG]: This function replaces the displayed number with the largest integer less than or equal to it.
-
[f][FRAC]: Extracts and displays the fractional part of the displayed number.
-
[g][RND]: Rounds the displayed number to the number of decimal places specified by the current display format (fixed point, scientific notation, or engineering notation).
-
[g][ABS]: Displays the absolute value of the number in the X register.
Example:
-
Enter: 123.4567
-
Press: [g][INTG] → Displays: 123.0000
-
Press: [f][FRAC] → Displays: 0.4567
-
Press: [g][RND] → Displays: 123.457 (assuming the display format is set to show three decimal places)
-
Press: [CHS] → Displays: -123.457
-
Press: [g][ABS] → Displays: 123.457
2.2.3. One-Number Functions
These functions operate on a single number in the X register.
2.2.3.1. General Functions:
-
[1/x]: Calculates the reciprocal of the displayed number.
-
[f][x!]: Calculates the factorial of the displayed integer value (x!), where 0 ≤ x ≤ 69. This function can also be used to compute the gamma function (Γ(x)) used in advanced mathematics and statistics, where x is not restricted to non-negative integers. To achieve this, use the formula Γ(x) = (x-1)!
-
[√x]: Calculates the positive square root of the displayed number.
-
[g][x²]: Squares the displayed number.
Examples:
-
Enter: 25
-
Press: [1/x] → Displays: 0.04
-
Enter: 8
-
Press: [f][x!] → Displays: 40320 (calculates 8!)
-
Enter: 3.9
-
Press: [√x]: → Displays: 1.9748
-
Enter: 12.3
-
Press: [g][x²] → Displays: 151.29
2.2.3.2. Trigonometric Functions
The DM15 supports calculations in three different angle units or trigonometric modes: Degrees, Radians, and Grads.
-
[g][DEG]: Sets the calculator to Degrees mode (default mode).
-
[g][RAD]: Sets the calculator to Radians mode, indicated by the "RAD" annunciator on the display.
-
[g][GRAD]: Sets the calculator to Grads mode, indicated by the "GRAD" annunciator on the display.
Note: Setting a specific trigonometric mode does not convert existing numbers in the calculator; it only determines the angle unit for subsequent trigonometric operations.
-
[SIN]: Calculates the sine of the displayed value.
-
[g][ASIN]: Calculates the arcsine of the displayed value.
-
[COS]: Calculates the cosine of the displayed value.
-
[g][ACOS]: Calculates the arccosine of the displayed value.
-
[TAN]: Calculates the tangent of the displayed value.
-
[g][ATAN]: Calculates the arctangent of the displayed value.
Important: Before performing any trigonometric calculations, ensure the calculator is set to the desired angle unit (Degrees, Radians, or Grads).
2.2.3.3. Time and Angle Conversions
The DM15 provides functions to convert values representing time or angles between decimal and sexagesimal formats:
-
[f][→HMS]: Converts a decimal value representing hours or degrees into hours, minutes, and seconds or degrees, minutes, and seconds format.
-
[g][→DEG]: Converts a value in hours, minutes, and seconds or degrees, minutes, and seconds format into a decimal value representing hours or degrees.
2.2.3.4. Logarithmic Functions
-
[g][LN]: Calculates the natural logarithm (base e) of the displayed number.
-
[eˣ]: Calculates the natural antilogarithm (e raised to the power of the displayed number).
-
[g][LOG]: Calculates the common logarithm (base 10) of the displayed number.
-
[10ˣ]: Calculates the common antilogarithm (10 raised to the power of the displayed number).
2.2.3.5. Hyperbolic Functions
-
[f][SINH]: Calculates the hyperbolic sine of the displayed value.
-
[g][ASINH]: Calculates the inverse hyperbolic sine of the displayed value.
-
[f][COSH]: Calculates the hyperbolic cosine of the displayed value.
-
[g][ACOSH]: Calculates the inverse hyperbolic cosine of the displayed value.
-
[f][TANH]: Calculates the hyperbolic tangent of the displayed value.
-
[g][ATANH]: Calculates the inverse hyperbolic tangent of the displayed value.
2.2.4. Two-Number Functions
These functions require two numbers to be present in the calculator. Remember to separate the two numbers with the [ENTER] key if you are entering them sequentially.
2.2.4.1. Power Function
-
[yˣ]: Raises the number in the Y register (entered first) to the power of the number in the X register (entered second).
2.2.4.2. Percentages
-
[g][%]: Computes a specified percentage of a base number. The base number is entered first, and the percentage is entered second.
-
[g][∆%]: Calculates the percentage change between two numbers. The original number is entered first, and the new number is entered second.
2.2.5. Coordinate Conversions
The DM15 allows you to convert between rectangular (x, y) and polar (r, θ) coordinates.
-
[g][→P]: Converts rectangular coordinates (x, y) to polar coordinates (r, θ). Enter the y-coordinate first, then the x-coordinate.
-
[f][→R]: Converts polar coordinates (r, θ) to rectangular coordinates (x, y). Enter the angle θ first, then the magnitude r.
Note: Ensure the calculator is in the appropriate trigonometric mode (Degrees, Radians, or Grads) before performing coordinate conversions.
This section has provided a comprehensive overview of the DM15’s numeric functions. As you become familiar with these functions, you’ll appreciate the versatility and power of this calculator. The next section will introduce the automatic memory stack, a crucial element of RPN calculators.
2.3. The Automatic Memory Stack, LASTx, and Data Storage
This section introduces the core of the DM15’s operational logic – the automatic memory stack, a fundamental feature of Reverse Polish Notation (RPN) calculators. Additionally, you’ll learn about the LASTx register and data storage operations, which enhance your calculation capabilities.
2.3.1. Automatic Memory Stack and Stack Manipulation
The DM15 employs RPN, a unique calculation approach where operators are entered after the operands. This eliminates the need for parentheses and simplifies complex calculations. The automatic memory stack plays a crucial role in this process by storing intermediate results and managing the flow of calculations.
2.3.1.1. Understanding the Stack Registers
The DM15 has four stack registers, labelled T, Z, Y, and X, organized as follows:
T: (Top of Stack)
Z:
Y:
X: (Displayed Register)
-
The X register, located at the bottom of the stack, is always displayed on the screen.
-
Any number you enter or any result from a calculation goes into the X register, causing the other numbers in the stack to move up one level (stack lift).
-
The stack operates on a "Last-In-First-Out" (LIFO) basis, meaning the last number entered is the first one used in the next operation.
2.3.1.2. Stack Manipulation Functions
The DM15 provides several functions to manage the stack effectively:
-
[ENTER]: This key duplicates the number in the X register and pushes it up into the Y register, effectively separating two numbers entered consecutively.
-
[R↓]: (Roll Down) Shifts the stack contents down one register. The number in the X register moves to the T register, the number in Y moves to X, and so on.
-
[R↑]: (Roll Up) Shifts the stack contents up one register. The number in the T register moves to X, the number in Z moves to T, and so on.
-
[x↔y]: Exchanges the values in the X and Y registers.
Example: Observe how the stack behaves when filled with the numbers 1, 2, 3, and 4:
-
Enter: 1
-
Press: [ENTER] → Stack: (T: -, Z: -, Y: 1, X: 1)
-
Enter: 2
-
Press: [ENTER] → Stack: (T: -, Z: 1, Y: 2, X: 2)
-
Enter: 3
-
Press: [ENTER] → Stack: (T: 1, Z: 2, Y: 3, X: 3)
-
Enter: 4 → Stack: (T: 2, Z: 3, Y: 4, X: 4)
-
Press: [R↓] → Stack: (T: 4, Z: 2, Y: 3, X: 4)
-
Press: [R↑] → Stack: (T: 2, Z: 3, Y: 4, X: 2)
-
Press: [x↔y] → Stack: (T: 2, Z: 3, Y: 2, X: 4)
2.3.2. LASTx Register and [LASTx]
The LASTx register is a separate memory location that stores the value last displayed in the X register before a calculation is performed. The [g][LASTx] key recalls this value back to the X register. This function is helpful for:
-
Reusing previous entries: If you need to use a number again in a calculation, simply press [g][LASTx] to retrieve it instead of re-entering it.
-
Error recovery: If you make a mistake during a calculation, [g][LASTx] can help you recover the previous value and correct the error.
Example:
-
Enter: 287
-
Press: [÷]
-
Enter: 12 (Oops! Meant to enter 13)
-
Press: [g][LASTx] → Displays: 12 (recalls the mistakenly entered divisor)
-
Press: [×] → Reverses the division
-
Enter: 13
-
Press: [÷]
-
The correct result is displayed
2.3.3. Calculator Functions and Stack Behavior
Understanding how different functions interact with the stack is crucial for mastering RPN calculations. Here’s a breakdown of their behavior:
-
Stack-Enabling Operations: Most functions, including one- and two-number mathematical operations, enable stack lift. This means that after performing such a function, entering a new number will automatically push the existing numbers in the stack up one level.
-
Stack-Disabling Operations: The following functions disable stack lift:
-
[ENTER]: While [ENTER] initially lifts the stack by copying the X register value to the Y register, it disables the lift for the subsequent entry. This ensures the next entered number replaces the value in the X register without affecting the rest of the stack.
-
[CLx]: As it clears the X register, it also disables the stack lift for the next entry.
-
[g][Σ+]: This function is related to statistical calculations (explained later) and also disables stack lift.
-
[g][Σ-]: Similar to [g][Σ+], this function is used in statistics and disables stack lift.
-
2.3.4. Order of Entry and the [ENTER] Key
When working with two-number functions, entering the numbers in the correct order (y-value first, then x-value) is important. This ensures the numbers are positioned correctly within the stack for the operation.
Example: To calculate 98 - 15:
-
Enter: 98 (This becomes the y-value in the Y register)
-
Press: [ENTER]
-
Enter: 15 (This becomes the x-value in the X register)
-
Press: [-]
-
The result (83) is displayed in the X register
2.3.5. Nested Calculations
The beauty of RPN and the automatic memory stack shines when dealing with nested calculations. You can solve complex expressions without parentheses or the need to store intermediate results. Simply work from the innermost parentheses outwards, entering numbers and performing operations as you encounter them.
Example: Calculate 3 [4 + 5 (6 + 7)]
-
Enter: 6
-
Press: [ENTER]
-
Enter: 7
-
Press: [+]
-
Enter: 5
-
Press: [×]
-
Enter: 4
-
Press: [+]
-
Enter: 3
-
Press: [×]
-
The final result (207) is displayed
2.3.6. Arithmetic Calculations with Constants
The DM15 offers several ways to efficiently perform repeated calculations with a constant value:
-
Using the LASTx register: Enter the constant as the second operand in a two-number function, so it is stored in the LASTx register. You can then use [g][LASTx] to recall the constant as needed for subsequent calculations.
-
Loading the stack with a constant: Fill the stack by entering the constant and pressing [ENTER] three times. Then, enter the variable operand and perform the desired operation. This method is useful when you have a series of different values to operate on with the same constant.
-
Accumulating calculations with a constant: Load the stack with a constant as described above, but instead of clearing the X register, keep the result of the operation and perform the same operation again. This effectively accumulates the result with each operation.
2.3.7. Storage Register Operations
The DM15 provides dedicated registers for storing and recalling numbers, allowing you to retain important values for later use.
2.3.7.1. Storing and Recalling Numbers
-
[STO]: Followed by a register number (0-9 or .0-.9), this function stores the current value in the X register into the specified storage register.
-
[RCL]: Followed by a register number (0-9 or .0-.9), this function recalls the value from the specified storage register and displays it in the X register.
-
[x↔y]: Followed by a register number (0-9 or .0-.9), this function exchanges the contents of the X register with the contents of the specified storage register.
2.3.7.2. Clearing Data Storage Registers
-
[f][CL REG]: Clears the contents of all data storage registers to zero.
-
Storing zero: To clear a specific storage register, simply store the value zero in that register.
-
Resetting Continuous Memory: This action clears all registers and the stack (explained in Section 5).
2.3.7.3. Storage and Recall Arithmetic
The DM15 allows you to perform arithmetic operations directly with stored values without the need to recall them first.
-
Storage Arithmetic: This function lets you perform an arithmetic operation with the current X register value and a stored value, then store the result back into the same storage register. The sequence is:
-
Ensure the second operand (the one not in storage) is in the X register.
-
Press [STO].
-
Press the desired arithmetic operation key ([+], [-], [×], [÷]).
-
Enter the storage register number.
-
-
Recall Arithmetic: This function performs an arithmetic operation with the current X register value and a stored value, then displays the result in the X register without affecting the stack. The sequence is:
-
Ensure the second operand (the one not in storage) is in the X register.
-
Press [RCL].
-
Press the desired arithmetic operation key ([+], [-], [×], [÷]).
-
Enter the storage register number.
-
2.3.8. Overflow and Underflow
The DM15 has limitations on the magnitude of numbers it can handle.
-
Overflow: If a calculation results in a number exceeding the calculator’s limit (9.999999999 × 10⁹⁹), the display will show the maximum value and start blinking. To clear this overflow condition, press [←] or [ON].
-
Underflow: If a calculation results in a number smaller than the calculator’s limit (1.000000000 × 10⁻⁹⁹), the calculator will replace it with zero.
With a solid understanding of the automatic memory stack and data storage operations, you can confidently tackle a wide range of calculations using the DM15. The next section will explore the calculator’s statistical functions, further expanding your analytical capabilities.
2.4. Statistics Functions
This section explores the statistical capabilities of your DM15 calculator. These functions allow you to analyze data sets, calculate probabilities, and perform regressions, providing valuable insights for various applications.
Important: Statistical calculations on the DM15 rely on the memory stack and require careful attention to the order of entering data.
2.4.1. Probability Calculations
The DM15 can calculate permutations and combinations, providing insights into the possible arrangements or selections within a set of items.
-
[f][nPr]: Calculates the number of permutations (arrangements) of y distinct items taken x at a time, where order matters. Enter the y-value first, then the x-value.
-
[g][nCr]: Calculates the number of combinations (selections) of y distinct items taken x at a time, where order does not matter. Enter the y-value first, then the x-value.
Examples:
-
Permutation: How many ways can you arrange 3 books on a shelf if you have 5 different books to choose from?
-
Enter: 5
-
Press: [ENTER]
-
Enter: 3
-
Press: [f][nPr]
-
The result (60) is displayed
-
-
Combination: How many different 4-card hands are possible from a standard 52-card deck?
-
Enter: 52
-
Press: [ENTER]
-
Enter: 4
-
Press: [g][nCr]
-
The result (270,725) is displayed
-
Note: Both x and y values in permutation and combination calculations must be non-negative integers less than 10¹⁰.
2.4.2. Random Number Generator
The DM15 features a random number generator that produces a sequence of pseudo-random numbers between 0 and 1.
-
[f][RND]: Generates a new random number and displays it.
Controlling the Random Number Sequence:
-
[STO][f][RND]: Stores the current X register value as the seed for the random number generator, influencing the subsequent sequence of random numbers.
-
[RCL][f][RND]: Recalls the current seed value to the X register.
2.4.3. Accumulating Statistics
The DM15 can perform one-variable and two-variable statistical calculations. Data is entered into the X and Y registers, and the [g][Σ+] function automatically calculates and stores statistical measures in dedicated storage registers (R2 to R7).
2.4.3.1. Initializing for Statistics
Before starting a new statistical analysis, it’s essential to clear the previous data and prepare the calculator. Press [f][CLΣ] to clear the statistics registers and the stack.
2.4.3.2. One-Variable Statistics
-
Enter each data point (x-value) and press [g][Σ+].
-
The current number of data points (n) will be displayed.
2.4.3.3. Two-Variable Statistics
-
Enter the y-value first.
-
Press: [ENTER]
-
Enter the x-value.
-
Press: [g][Σ+]
-
The current number of data pairs (n) will be displayed.
2.4.3.4. Accessing Accumulated Statistics
-
[RCL] followed by the corresponding register number (2-7) recalls a specific statistical value.
-
[RCL][g][Σ+] recalls Σx (sum of x values) to the X register and Σy (sum of y values) to the Y register simultaneously.
Statistics Registers:
-
R2: n (number of data points)
-
R3: Σx (sum of x values)
-
R4: Σx² (sum of squared x values)
-
R5: Σy (sum of y values)
-
R6: Σy² (sum of squared y values)
-
R7: Σxy (sum of x*y products)
2.4.3.5. Correcting Accumulated Statistics
-
[g][Σ-]: To remove the last entered data point or data pair from the accumulated statistics, enter the incorrect value(s) and press [g][Σ-]. You can then enter the correct data and press [g][Σ+].
-
Alternative: If the incorrect data was the most recently entered and [g][Σ+] was pressed, use [g][LASTx][g][Σ-] to remove it.
2.4.4. Statistical Calculations
Once you’ve accumulated the necessary data, the DM15 allows you to perform various statistical calculations.
-
[g][$\bar{x}$]: Calculates the mean (average) of the x-values and y-values. The mean of x is placed in the X register, and the mean of y is placed in the Y register.
-
[g][σx]: Calculates the sample standard deviation of the x-values and y-values. The standard deviation of x is placed in the X register, and the standard deviation of y is placed in the Y register.
-
[f][L.R.]: Performs linear regression to find the best-fit line for the data. The y-intercept is placed in the X register, and the slope is placed in the Y register.
-
[f][ŷ]: Calculates the predicted y-value (ŷ) for a given x-value based on the linear regression analysis. The correlation coefficient (r) is also calculated and stored in the Y register.
Note: For more advanced statistical analysis, refer to the dedicated statistical functions manual.
With these statistical functions, the DM15 becomes a powerful tool for analyzing data and uncovering valuable insights. The next section will discuss display control and the continuous memory feature, further enhancing your user experience.
2.5. Display and Continuous Memory
This section covers the different display formats available on the DM15 and how to customize them to suit your preferences. Additionally, you’ll learn about the Continuous Memory feature that preserves your data and settings even when the calculator is powered off.
2.5.1. Display Control
The DM15 offers three distinct display formats: Fixed Point, Scientific Notation, and Engineering Notation. Each format allows you to specify the number of decimal places to be displayed.
-
Fixed Point: This format displays numbers with a fixed number of decimal places, ideal for everyday calculations. To set the number of decimal places, use [f][FIX] followed by the desired number of digits (0-9).
-
Scientific Notation: This format displays numbers in scientific notation, suitable for very large or very small values. Use [f][SCI] followed by the desired number of digits (0-9) to set the precision.
-
Engineering Notation: Similar to scientific notation, this format displays numbers with exponents in multiples of three, aligning with standard engineering units. Use [f][ENG] followed by the desired number of digits (0-9) to set the precision.
2.5.2. Understanding Display Precision and Internal Representation
While the display formats allow you to control the number of decimal places shown on the screen, the DM15 internally stores all numbers with a 10-digit mantissa and a 2-digit exponent. This ensures high precision in calculations even if the displayed value is rounded.
-
Viewing the Full Mantissa: To see all 10 digits of the mantissa, press and hold [f][CLx].
2.5.3. Round-Off Error
Due to the finite precision of the calculator, rounding errors may occur during calculations, especially in lengthy or complex operations. These errors are usually insignificant but it’s essential to be aware of their potential impact, especially when dealing with extremely precise measurements.
2.5.4. Special Displays
2.5.4.1. Annunciators
The DM15 uses annunciators to indicate various calculator states and modes:
-
Low Battery: A battery symbol (☆) appears in the lower-left corner when the batteries need replacing.
-
USER: Indicates User mode is active (explained in Part II of the manual).
-
f and g: Show the current prefix state for accessing alternate functions.
-
RAD and GRAD: Indicate the current trigonometric mode (Radians or Grads).
-
PRGM: Indicates you are in Program mode for entering or editing programs.
2.5.4.2. Digit Separators
By default, the DM15 separates the integer and fractional parts of a number with a period (decimal point) and groups of three digits in the integer part with a comma. To change this to a comma for the decimal separator and a period for digit grouping (common in some regions), perform the following steps with the calculator turned off:
-
Press and hold [ON].
-
Press and hold [.].
-
Release [ON].
-
Release [.].
Repeat this process to switch back to the default setting.
2.5.4.3. Error Display
If an error occurs during a calculation, the display will show "Error" followed by a number indicating the type of error. Refer to the specific error codes and their meanings in the appendix of this manual. To clear the error message and return to the previous state, press any key.
2.5.4.4. Overflow and Underflow
-
Overflow: When a calculation result exceeds the calculator’s maximum limit, the display shows the maximum value and blinks. Press [←] or [ON] to clear this condition.
-
Underflow: When a calculation results in a value smaller than the calculator’s minimum limit, it is replaced with zero.
2.5.5. Continuous Memory
The DM15 features Continuous Memory, which preserves the following data and settings even when the calculator is turned off:
-
All numeric data stored in registers
-
All programs stored in memory
-
Calculator’s position in program memory
-
Display format and settings
-
Trigonometric mode
-
Pending subroutine returns
-
Flag settings
-
User mode setting
Resetting Continuous Memory:
To clear all data and reset the calculator to its default state, follow these steps:
-
Turn off the calculator.
-
Press and hold [ON], then press and hold [←].
-
Release [ON], then release [←].
The display will show "MEMORY CLEAR" indicating Continuous Memory has been reset. Press any key to clear this message.
Caution: Continuous Memory can be inadvertently reset if the calculator is subjected to a strong impact or shock.
With the ability to customize the display and the reassurance of Continuous Memory, you can utilize the DM15 to its full potential. The next part of the manual will delve into the exciting realm of programming this powerful calculator.
3. Programming
3.1. Programming Basics
This section marks the beginning of your journey into programming the DM15. It covers the fundamentals of creating, storing, and running programs, empowering you to automate calculations and solve problems with greater efficiency.
3.1.1. Programming Concepts
The DM15 utilizes keystroke programming, where the steps you would typically perform manually are recorded as a program. This approach makes programming intuitive and easy to learn, even for users without prior programming experience.
3.1.2. Entering Programming Mode
To begin creating a program, press [PRGM]. The display will show "000-" indicating you are in Program mode and ready to enter instructions.
3.1.3. Program Memory and Line Numbers
Program instructions are stored in the DM15’s memory, organized sequentially by line numbers. Line 000 marks the start of program memory but cannot store instructions. The first usable line is 001.
-
Navigating Program Memory:
-
[GTO] [000]: Jumps to line 000 without recording the jump as an instruction.
-
[f][CLx]: In normal operation, it resets the program counter to line 000 without clearing memory. During program editing, it clears the entire program memory.
-
3.1.4. Creating a Program
-
Start at Line 000: Ensure you are at the beginning of the program memory by using one of the methods mentioned above.
-
Label the Program (Optional): Assigning a label to your program allows you to easily identify and run it later. Use [LBL] A-E, 0-9, or .0-.9 to create a label. For example, [LBL] A labels the program as "A".
-
Enter Program Instructions: Now, input the desired sequence of keystrokes for your calculation, just as you would perform it manually. Each keystroke, including numbers, operators, and functions, will be stored as a program instruction.
-
End the Program: To signify the end of your program, use one of the following options:
-
[RTN]: This instruction ends the program, returns the program counter to line 000, and halts execution.
-
[R/S]: This instruction stops the program at its current line without returning to line 000. You can resume execution later by pressing [R/S] from the keyboard in Run mode.
-
Reaching the End of Memory: If you fill the available program memory, the calculator automatically inserts a [RTN] instruction at the end.
-
3.1.5. Running a Program
-
Enter Run Mode: Press [PRGM] to exit Program mode and enter Run mode.
-
Enter Data (if necessary): If your program requires input values, enter them now.
-
Execute the Program:
-
[f] A-E, 0-9, or .0-.9: To run a labeled program, press [f] followed by the program label.
-
[GTO] A-E, 0-9, or .0-.9: Alternatively, you can use the [GTO] key followed by the label to run a program.
-
3.1.6. Program Control Flow
-
[f][PSE]: The pause instruction temporarily halts program execution for approximately one second, allowing you to view intermediate results. Use multiple [f][PSE] instructions for longer pauses.
-
User Mode: This mode can save keystrokes when running programs labelled with letters (A-E). Pressing [f][USER] will swap the primary and [f]-shifted functions of the A-E keys. You can then execute the program by simply pressing the corresponding letter key.
3.1.7. Program Memory Management
The DM15’s memory is shared between data storage and program instructions. The initial configuration allocates 21 registers for data and 78 registers for programs and advanced functions. You can adjust this allocation using the [g][P←R] and [g][R←P] functions to balance your data storage and programming needs. Refer to the appendix for detailed information on memory management.
Note:
-
Each register holds 7 bytes of memory.
-
Most program instructions use 1 byte, while some require 2 bytes (see the appendix for a list).
-
The maximum program memory capacity is 672 bytes.
-
If you encounter an "Error 10" message, it indicates insufficient memory. You may need to reallocate registers or optimize your program to use less memory.
3.1.8. Programming Tips
-
Horner’s Method: For evaluating polynomial expressions, Horner’s method can reduce the number of calculations and improve efficiency.
-
Data Entry: Consider how your program will receive input values. You can either enter data before running the program or include pauses ([f][PSE]) within the program to allow data entry during execution.
3.1.9. Non-Programmable Functions
While most functions can be used within programs, the following functions cannot be directly recorded as program instructions:
-
[f][CLx]
-
[g][P←R]
-
[g][R←P]
-
[f][USER]
-
[GTO] nnn (where nnn is a line number)
-
[←]
-
[ON]
With this foundation in programming basics, you are equipped to start creating your own programs on the DM15. The following sections will explore more advanced programming techniques and functions, allowing you to unlock the full potential of this remarkable calculator.
3.2. Program Editing
Inevitably, you’ll find the need to modify or correct programs after you’ve created them. This section explores the editing functionalities of the DM15, enabling you to refine and perfect your programs with ease.
3.2.1. Navigating Program Memory
Before making any edits, you need to locate the specific line within your program that requires modification. The DM15 provides several methods for navigating program memory:
-
[GTO] nnn: This command directly jumps to the specified line number (nnn). It is not a programmable instruction but a manual navigation tool.
-
[SST]: (Single Step) Advances the program counter forward one line at a time. This function is not programmable.
-
In Program Mode: Pressing [SST] displays the next program instruction without executing it. Holding the key continuously scrolls through the program.
-
In Run Mode: Holding [SST] displays the current program line. Releasing the key executes the instruction and advances to the next line.
-
-
[BST]: (Back Step) Moves the program counter back one line. This function is not programmable. Pressing and holding [BST] allows you to scroll backward through the program without executing instructions.
3.2.2. Editing Program Lines
3.2.2.1. Deleting Lines
-
[←]: In Program mode, pressing [←] deletes the entire instruction displayed on the current line. Subsequent lines automatically renumber to maintain sequential order.
Important: Remember, [←] functions differently in Run mode, where it acts as a backspace or clear key depending on the context.
3.2.2.2. Inserting Lines
-
Position the Cursor: Use the navigation methods mentioned above to move to the line before where you want to insert the new instruction.
-
Enter the New Instruction: Simply key in the desired instruction as you would during program creation. The new instruction will be inserted after the currently displayed line, and subsequent lines will be renumbered.
3.2.2.3. Modifying Lines
To modify an existing instruction, first delete it using [←] and then insert the corrected instruction as described above.
3.2.3. Example: Program Editing
Let’s revisit the example program from Section 6 that calculated the volume and surface area of cylindrical cans. Suppose we want to modify the program to eliminate the calculation and display of the surface area.
Original Program (excerpt):
006 LBL A 007 STO 0 (Store radius in R0) 008 g x² (Square the radius) 009 g π (Multiply by pi) 010 STO 4 (Store base area in R4) ... 018 RCL 4 (Recall base area) 019 × 2 (Multiply by 2 for top and bottom) 020 + (Add side area to get surface area)
Editing Steps:
-
Enter Program mode and navigate to line 018 ([GTO] 018 or use [SST]).
-
Delete lines 018, 019, and 020 using [←] three times.
-
The program should now look like this:
017 × 2 (Calculate 2πrh) 018 RTN (End of program)
With these editing capabilities, you can easily refine and adapt your programs as needed. Remember to save your modified programs using Continuous Memory to avoid losing your work when the calculator powers off.
3.2.4. Additional Notes
-
Single-Stepping for Debugging: If your program encounters errors or behaves unexpectedly, you can use single-stepping ([SST]) in Run mode to execute the program line by line and observe the results, helping you identify and correct any issues.
-
Memory Limitations: If you attempt to insert instructions but encounter an "Error 4" message, it means the program memory is full. You may need to delete some instructions or reallocate memory to create space for new instructions.
-
Initializing Program State: It’s good practice to initialize relevant settings and clear storage registers at the beginning of your program or before running it to ensure consistent and predictable results.
Mastering program editing techniques is crucial for developing efficient and reliable programs on the DM15. As you continue exploring the programming capabilities of this calculator, you’ll discover its immense potential for solving complex problems and automating your calculations. The next section will introduce branching and control structures, further enhancing the power and flexibility of your programs.
3.3. Program Branching and Controls
This section introduces branching and control structures, essential tools for creating more complex and dynamic programs on your DM15 calculator. These features allow you to control the flow of execution, making decisions and repeating instructions based on specific conditions.
3.3.1. Branching
Branching allows you to alter the sequential execution of instructions and jump to different parts of your program.
-
Unconditional Branching:
-
[GTO] Label: This instruction transfers program execution to the line labelled with the specified label (A-E, 0-9, or .0-.9). The program then continues from that point onwards.
-
-
Looping:
-
[GTO] Label (where the label refers to a previous line): This creates a loop, repeatedly executing the instructions between the [GTO] instruction and the labelled line. Loops can be controlled using conditional tests or manually interrupted by pressing any key during execution.
-
3.3.2. Conditional Tests
Conditional tests allow your program to make decisions based on specific conditions. The DM15 provides several ways to perform these tests:
-
Direct Comparison Tests:
-
[x=y]: Tests if the values in the X and Y registers are equal.
-
[x≠y]: Tests if the values in the X and Y registers are not equal.
-
-
Indirect Comparison Tests:
-
[g][x?]y: Provides a range of comparison tests between the X register value and the Y register value. Enter the desired test number (0-9) after pressing [g][x?].
-
0: x ≠ 0
-
1: x > 0
-
2: x < 0
-
3: x ≥ 0
-
4: x ≤ 0
-
5: x = y
-
6: x ≠ y
-
7: x > y
-
8: x < y
-
9: x ≥ y
-
-
-
"Do if True" Rule: For all conditional tests, the program executes the next instruction if the condition is true. If the condition is false, the program skips the next instruction and continues from the following line.
3.3.3. Flags
Flags are like switches that can be set or cleared to indicate specific conditions within your program. The DM15 provides eight user flags (0-7) and two system flags (8 and 9):
-
Setting Flags: [f][FLAG] n sets flag number n.
-
Clearing Flags: [f][SF] n clears flag number n.
-
Testing Flags: [f][FS?] n tests if flag number n is set (true).
-
System Flags:
-
Flag 8: Indicates Complex mode is active.
-
Flag 9: Indicates an overflow condition.
-
3.3.4. Examples
3.3.4.1. Branching and Looping
Example: Create a program to calculate the factorial of a number using a loop.
000 LBL A (Start of program) 001 STO 0 (Store input number in R0) 002 1 (Initialize counter) 003 LBL B (Start of loop) 004 RCL 0 (Recall number) 005 × (Multiply by counter) 006 STO 0 (Store intermediate result) 007 RCL 0 (Recall counter) 008 DSE 0 (Decrement and skip if zero) 009 GTO B (Loop back if counter is not zero) 010 RTN (End of program)
Explanation:
-
The program starts by storing the input number (n) in register R0 and initializing a counter to 1.
-
The loop begins at label B. It multiplies the current value in R0 by the counter and stores the result back in R0.
-
The counter is decremented, and the program skips the next instruction (GTO B) if the counter reaches zero.
-
If the counter is not zero, the program jumps back to label B and repeats the loop.
-
Once the counter reaches zero, the loop terminates, and the program ends, leaving the factorial of n in register R0.
3.3.4.2. Flags
Example: Modify the factorial program to calculate the factorial only for positive integers. Use a flag to indicate if the input is valid.
000 LBL A (Start of program) 001 f SF 0 (Clear flag 0) 002 x≥0? (Test if input is non-negative) 003 GTO B (Skip initialization if input is negative) ... (rest of the program is the same as before)
Explanation:
-
The program starts by clearing flag 0.
-
The conditional test checks if the input number in the X register is non-negative (x ≥ 0). If true, the program continues to the loop initialization (line 003). If false, the program skips the initialization and proceeds to the end.
-
The rest of the factorial calculation remains the same as before.
3.3.5. Additional Notes
-
Nested Loops: You can create loops within loops to handle more complex iterative processes.
-
Conditional Branching: Use conditional tests in conjunction with branching instructions ([GTO]) to create conditional branches, directing the program flow based on specific criteria.
-
Multiple Conditions: Combine multiple conditional tests using flags and logic to implement more sophisticated decision-making within your programs.
Branching and control structures greatly enhance the capabilities of your DM15 programs. By incorporating these features, you can create dynamic and adaptable programs to solve a wide range of problems. The next section will delve into the Index register and loop control techniques, further expanding your programming skills.
3.4. Subroutines
This section introduces the concept of subroutines in DM15 programming. Subroutines are self-contained blocks of code that can be called from various points within your main program, promoting code reusability and modularity.
3.4.1. Understanding Subroutines
Imagine having a set of instructions that needs to be executed multiple times within your program. Instead of repeating those instructions at each instance, you can create a subroutine – a separate block of code containing those instructions – and call it whenever needed.
3.4.2. Creating and Calling Subroutines
-
Define the Subroutine:
-
Start with a label: Use [LBL] Label (A-E, 0-9, or .0-.9) to assign a unique label to your subroutine.
-
Enter instructions: Input the desired sequence of keystrokes for the subroutine’s functionality.
-
End with [RTN]: Use the [RTN] instruction to signify the end of the subroutine and return control to the calling point in the main program.
-
-
Call the Subroutine:
-
[GTO] Label: Within your main program, use [GTO] followed by the subroutine’s label to transfer execution to the subroutine.
-
3.4.3. Subroutine Return Mechanism
The [RTN] instruction at the end of a subroutine is crucial. It does more than just end the subroutine; it also remembers the location in the main program from where the subroutine was called and returns control to that point, ensuring the main program continues seamlessly.
3.4.4. Nested Subroutines
The DM15 allows you to call one subroutine from within another, creating nested subroutine structures. This can be useful for breaking down complex tasks into smaller, more manageable sub-tasks. However, be mindful of the nesting limit – you can nest subroutines up to seven levels deep.
Note: Exceeding the nesting limit will result in an "Error 5" message.
3.4.5. Example: Using Subroutines
Let’s create a program to calculate the area of a triangle using Heron’s formula, where s is the semi-perimeter, and a, b, and c are the side lengths:
Area = √(s(s-a)(s-b)(s-c))
We can create a subroutine to calculate the semi-perimeter (s) and call it twice within the main program.
Main Program:
000 LBL A (Start of main program) 001 STO 0 (Store side a in R0) 002 STO 1 (Store side b in R1) 003 STO 2 (Store side c in R2) 004 GTO B (Call subroutine to calculate s) 005 STO 3 (Store s in R3) 006 GTO B (Call subroutine again to reuse a, b, c) 007 RCL 3 (Recall s) 008 - (Subtract) 009 RCL 0 (Recall a) 010 × (Multiply by (s-a)) ... (similar calculations for (s-b) and (s-c)) 017 √x (Calculate square root to get area) 018 RTN (End of main program) *Subroutine (calculate s):* 019 LBL B (Start of subroutine) 020 RCL 0 (Recall a) 021 RCL 1 (Recall b) 022 + (Add a and b) 023 RCL 2 (Recall c) 024 + (Add c to get perimeter) 025 2 (Divide by 2 to get semi-perimeter s) 026 ÷ (s is now in the X register) 027 RTN (Return to main program)
Explanation:
-
The main program stores the side lengths (a, b, c) in registers R0, R1, and R2.
-
It calls the subroutine labelled "B" to calculate the semi-perimeter (s) using the stored side lengths.
-
The calculated value of s is stored in R3 for later use.
-
The subroutine is called again, taking advantage of the fact that the side lengths are still in the stack from the previous call. This second call is simply to reuse the values and position them correctly in the stack for the subsequent calculations.
-
The main program then performs the calculations according to Heron’s formula using the stored value of s and the side lengths.
-
Finally, the program calculates the square root to obtain the area of the triangle.
3.4.6. Advantages of Using Subroutines
-
Code Reusability: Subroutines avoid code duplication, making your programs more concise and efficient.
-
Modularity: Subroutines break down complex tasks into smaller, more manageable units, improving code organization and readability.
-
Maintainability: Changes to a particular calculation or process can be made within the subroutine without affecting the main program, simplifying program maintenance.
Subroutines are a valuable tool for creating well-structured and efficient programs on the DM15. By understanding their use and advantages, you can significantly enhance your programming capabilities. The next section will explore the Index register and its role in controlling loop execution, providing even greater flexibility for your programs.
3.5. The Index Register and Loop Control
This section introduces the Index register, a powerful tool for advanced programming on the DM15. You’ll learn how to use it for indirect addressing, loop control, and other advanced operations, significantly expanding your programming capabilities.
3.5.1. Understanding the Index Register
The Index register, denoted as "I" or "RI", is a special data storage register that serves a dual purpose:
-
Direct Data Storage: You can store and recall numerical values directly into the Index register, similar to other data storage registers.
-
Indirect Addressing: The Index register can act as a pointer to access other data storage registers and control program flow indirectly.
3.5.2. Accessing the Index Register
-
Direct Storage and Recall:
-
[STO] I: Stores the value in the X register into the Index register.
-
[RCL] I: Recalls the value from the Index register and displays it in the X register.
-
-
Indirect Addressing:
-
[STO] (i): Stores the value in the X register into the data storage register pointed to by the Index register. For example, if the Index register contains the value 3, [STO] (i) stores the X register value into data storage register R3.
-
[RCL] (i): Recalls the value from the data storage register pointed to by the Index register and displays it in the X register.
-
3.5.3. Loop Control with the Index Register
The Index register, along with the [DSZ] (Decrement and Skip if Zero) and [ISG] (Increment and Skip if Greater) functions, provides a powerful mechanism for controlling loop execution.
Loop Counter Structure:
The loop counter is a number stored in a register (including the Index register) with the following format:
nnnnn.xxxyy
Where:
-
nnnnn: The current counter value (integer part).
-
xxx: The loop limit or test value (first three digits of the fractional part).
-
yy: The increment or decrement value (last two digits of the fractional part).
Example: 00003.01001 represents a loop counter starting at 3, incrementing by 1 with each iteration, and terminating when the counter exceeds 10.
Loop Control Functions:
-
[f][ISG] Register: This instruction increments the counter value in the specified register by the increment value (yy). If the new counter value is greater than the test value (xxx), the program skips the next instruction; otherwise, it continues sequentially.
-
[f][DSZ] Register: This instruction decrements the counter value in the specified register by the decrement value (yy). If the new counter value is zero or negative, the program skips the next instruction; otherwise, it continues sequentially.
3.5.4. Indirect Branching and Control
The Index register can also be used to control program flow indirectly:
-
[GTO] (i): Transfers program execution to the subroutine whose label corresponds to the value in the Index register. For example, if the Index register contains 2, the program jumps to the subroutine labelled "2".
-
[GTO] (i) (with a negative value in I): Branches to the program line number specified by the absolute value of the integer part of the number in the Index register.
-
Indirect Flag Control: Use [f][FLAG] (i), [f][SF] (i), and [f][FS?] (i) to set, clear, or test the flag number specified by the value in the Index register.
-
Indirect Display Format Control: Use [f][FIX] (i), [f][SCI] (i), and [f][ENG] (i) to set the display format using the value in the Index register for the number of decimal places.
Important Note: When using indirect addressing with (i), only the integer part of the value in the Index register is considered.
3.5.5. Advantages of the Index Register
-
Flexibility: Allows accessing and manipulating data and program flow indirectly, providing more versatile programming options.
-
Dynamic Loop Control: Enables creating loops with varying limits and increments, enhancing program adaptability.
-
Code Efficiency: Reduces code size by eliminating the need to repeatedly specify register numbers or line numbers.
3.5.6. Example: Using the Index Register for Loop Control
Program: Print the squares of numbers from 1 to 10.
000 LBL A (Start of program) 001 1 (Initialize counter) 002 STO I (Store counter in Index register) 003 LBL B (Start of loop) 004 RCL (i) (Recall number from register pointed to by I) 005 g x² (Square the number) 006 PSE (Pause to display the result) 007 ISG I (Increment and skip if greater) 008 GTO B (Loop back if counter <= 10) 009 RTN (End of program)
Explanation:
-
The program initializes the counter to 1 and stores it in the Index register.
-
The loop starts at label B. It recalls the value from the data storage register pointed to by the Index register (initially R1 since the counter is 1), squares it, and pauses to display the result.
-
The [ISG] I instruction increments the counter in the Index register. If the new counter value is greater than 10, the program skips the next instruction (GTO B) and terminates. Otherwise, the program jumps back to label B and continues the loop.
3.5.7. Mastering the Index Register
By incorporating the Index register into your programming toolkit, you can create more flexible and dynamic programs on the DM15. Its ability to control program flow and data access indirectly opens up a world of possibilities for solving complex problems and automating your calculations.
4. Advanced Functions
4.1. Calculating with Complex Numbers
This section explores the DM15’s capabilities for performing calculations with complex numbers, expanding your mathematical toolkit for advanced applications. You’ll learn how to enter, manipulate, and perform operations with complex numbers using the calculator’s dedicated functions and Complex mode.
4.1.1. Understanding Complex Numbers
Complex numbers are numbers of the form a + bi, where:
-
a is the real part.
-
b is the imaginary part.
-
i is the imaginary unit, defined as √(-1).
4.1.2. Entering Complex Mode
-
[f][CPLX]: Pressing this key activates Complex mode, indicated by the "CPLX" annunciator on the display. This mode enables the calculator to handle complex numbers and creates a separate stack for the imaginary parts.
4.1.3. Entering Complex Numbers
-
Enter the real part (a) of the complex number.
-
Press [ENTER].
-
Enter the imaginary part (b) of the complex number.
-
Press [f][CPLX] (if not already in Complex mode). This stores the complex number in the X register, with the real part in the real X register and the imaginary part in the imaginary X register.
Example: To enter the complex number 2 + 3i:
-
Enter: 2
-
Press: [ENTER]
-
Enter: 3
-
Press: [f][CPLX]
4.1.4. Complex Number Operations
Most arithmetic and mathematical functions on the DM15 work with complex numbers in Complex mode. The calculator automatically performs operations on both the real and imaginary parts, providing the result in complex form.
Examples:
-
Addition: (2 + 3i) + (4 + 5i) = 6 + 8i
-
Subtraction: (7 + 2i) - (1 + 6i) = 6 - 4i
-
Multiplication: (2 + 3i) * (4 + 5i) = -7 + 22i
-
Division: (8 + 4i) / (2 + i) = 4 + 2i
-
Square Root: √(4 + 3i) = 2 + i
Note: Trigonometric functions in Complex mode operate in radians, regardless of the current angle mode setting.
4.1.5. Stack Operations with Complex Numbers
-
[ENTER]: Duplicates the complex number in the X register and pushes it to the Y register, similar to real number operations.
-
[R↓] and [R↑]: Roll the contents of both the real and imaginary stacks down or up one register.
-
[x↔y]: Exchanges the complex numbers in the X and Y registers, swapping both real and imaginary parts.
4.1.6. Additional Complex Number Functions
-
[f][→R]: This function converts a complex number from polar form (magnitude and angle) to rectangular form (a + bi).
-
[g][→P]: This function converts a complex number from rectangular form to polar form.
-
[f][CONJ]: Calculates the complex conjugate of the complex number in the X register. The complex conjugate of a + bi is a - bi.
Note: For advanced operations with complex numbers and detailed explanations, refer to the dedicated complex number functions manual.
By mastering complex number calculations on the DM15, you open doors to more advanced mathematical and engineering applications. The next section will explore matrix operations, further expanding your problem-solving capabilities.
4.2. Calculating with Matrices
This section introduces the matrix capabilities of the DM15, allowing you to perform operations on matrices and solve systems of linear equations efficiently.
4.2.1. Understanding Matrices
A matrix is a rectangular array of numbers arranged in rows and columns. The DM15 can handle matrices with dimensions up to 8x8 and allows operations on up to five matrices, labelled A through E.
4.2.2. Dimensioning Matrices
-
Enter Dimensions: Enter the number of rows, then press [ENTER], and enter the number of columns.
-
Assign to Matrix: Press [f][DIM] followed by the letter (A-E) to assign the dimensions to the corresponding matrix.
Example: To dimension matrix A as a 3x4 matrix:
-
Enter: 3
-
Press: [ENTER]
-
Enter: 4
-
Press: [f][DIM] A
4.2.3. Entering and Recalling Matrix Elements
-
[g][MATRIX]: This function allows you to access individual matrix elements for storing and recalling values.
-
Storing Values: Enter the value, then press [ENTER], enter the row number, press [ENTER], and enter the column number. Finally, press [STO] [g][MATRIX] followed by the matrix letter (A-E).
-
Recalling Values: Enter the row number, press [ENTER], and enter the column number. Finally, press [RCL] [g][MATRIX] followed by the matrix letter (A-E).
-
-
User Mode: To efficiently input or recall all elements of a matrix sequentially, activate User mode by pressing [f][USER]. Then, enter the values or press [RCL] consecutively, and the row and column indices will automatically increment with each operation.
4.2.4. Matrix Operations
The DM15 provides a range of functions for performing operations on matrices:
-
Arithmetic Operations:
-
[+], [-], [×]: These functions perform matrix addition, subtraction, and multiplication, respectively. Ensure the matrices have compatible dimensions for these operations.
-
Scalar Multiplication: To multiply a matrix by a scalar (a single number), simply enter the scalar, press [ENTER], enter the matrix descriptor (e.g., "A"), and then press the desired arithmetic operation ([×] for multiplication).
-
-
Matrix Inverse:
-
[1/x]: Calculates the inverse of the matrix whose descriptor is in the X register.
-
-
Transpose:
-
[f][x<>y]: Calculates the transpose of the matrix whose descriptor is in the X register.
-
-
Determinant:
-
[f][DET]: Calculates the determinant of the matrix whose descriptor is in the X register.
-
-
Other Functions:
-
[f][FILL]: Fills all elements of a matrix with a specified value. Enter the value, then press [STO] [f][FILL] followed by the matrix letter.
-
[f][IDENTITY]: Creates an identity matrix with specified dimensions. Enter the dimension, then press [STO] [f][IDENTITY].
-
4.2.5. Solving Systems of Linear Equations
The DM15 efficiently solves systems of linear equations represented in matrix form as AX = B, where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.
-
Enter Matrices: Input the elements of matrices A and B using the methods described above.
-
Solve Equation: Enter the matrix descriptor for B, then press [ENTER], enter the matrix descriptor for A, and finally press [÷]. The solution matrix X will be calculated and stored in the designated result matrix.
Note: For more advanced matrix operations and complex matrices, refer to the dedicated matrix functions manual.
With these matrix capabilities, the DM15 becomes a powerful tool for tackling complex mathematical and engineering problems involving matrices and systems of linear equations.
4.3. Finding Roots of Equations
This section explores the root-finding capabilities of the DM15 using the [f][SOLVE] function. This powerful feature allows you to numerically estimate the roots (solutions) of equations where finding analytical solutions might be difficult or impossible.
4.3.1. Understanding Roots
A root of an equation f(x) = 0 is a value of x that makes the equation true. In other words, it’s the point where the graph of the function intersects the x-axis.
4.3.2. Using the [f][SOLVE] Function
The [f][SOLVE] function employs an iterative numerical method to approximate the roots of equations. Here’s how to use it:
-
Write a Function Subroutine:
-
Enter Program mode and create a subroutine that evaluates the function f(x) for a given value of x. The subroutine should start with a label (e.g., [LBL] A) and end with the calculated function value in the X register and a [RTN] instruction.
-
-
Provide Initial Guesses:
-
In Run mode, enter two initial guesses for the root, separated by [ENTER]. These guesses provide a starting point for the [f][SOLVE] algorithm and should ideally bracket the root (one guess below and one above the root).
-
-
Execute [f][SOLVE]:
-
Press [f][SOLVE] followed by the label of your function subroutine (e.g., [f][SOLVE] A).
-
The calculator will iterate through calculations, refining the estimate of the root until it reaches a satisfactory level of accuracy or encounters a condition that halts the process.
-
-
Interpret Results:
-
If a root is found, it will be displayed in the X register.
-
The Y register will contain a previous estimate of the root, and the Z register will contain the function value at the found root (ideally close to zero).
-
If no root is found or an error occurs, the calculator will display an error message.
-
4.3.3. Choosing Initial Guesses
The success and efficiency of [f][SOLVE] depend heavily on the quality of your initial guesses. Here are some tips for choosing them effectively:
-
Domain Knowledge: Consider the nature of the problem and the acceptable range of values for the root.
-
Function Behavior: If you have an understanding of the function’s behavior, choose guesses that are close to the root or bracket it.
-
Graphical Analysis: Plotting the function can provide visual insights into the approximate location of the roots.
-
Trial and Error: If you have no prior knowledge, try different guesses and observe the results to narrow down the search range.
4.3.4. Potential Issues and Error Messages
-
Error 8: No Root Found: This error indicates that the algorithm could not find a root within the specified range or encountered a situation where further refinement was not possible (e.g., function with a horizontal asymptote).
-
Error 0: Improper Math Operation: This error suggests an issue within your function subroutine, such as division by zero or taking the square root of a negative number.
-
Multiple Roots: If the equation has multiple roots, you’ll need to provide different sets of initial guesses to find them.
-
Root Accuracy: The accuracy of the found root depends on the function’s characteristics and the calculator’s precision. Be aware of potential round-off errors, especially when dealing with sensitive calculations.
4.3.5. Additional Techniques
-
Deflation: Once a root is found, you can modify the function subroutine to "deflate" it, removing the found root and allowing you to search for other roots more easily.
-
Analyzing Results: Pay close attention to the values in the Y and Z registers after using [f][SOLVE]. The function value in the Z register should ideally be close to zero, indicating a valid root.
The [f][SOLVE] function is a valuable tool for tackling equations that are challenging or impossible to solve analytically. By understanding its operation and limitations, you can effectively find roots and expand your problem-solving capabilities using the DM15. The next section will introduce numerical integration, another powerful mathematical tool available on this versatile calculator.
4.4. Numerical Integration
This section explores the numerical integration capabilities of the DM15 using the [f][∫] function. This powerful feature allows you to approximate the definite integral of a function, providing a valuable tool for solving problems in various fields such as physics, engineering, and statistics.
4.4.1. Understanding Definite Integrals
The definite integral of a function f(x) over an interval [a, b] represents the signed area between the curve of the function and the x-axis within that interval. It is denoted as:
∫(from a to b) f(x) dx
4.4.2. Using the [f][∫] Function
The [f][∫] function employs an iterative numerical method to approximate the definite integral of a function. Here’s how to use it:
-
Write a Function Subroutine:
-
In Program mode, create a subroutine that evaluates the function f(x) for a given value of x. The subroutine should start with a label (e.g., [LBL] A) and end with the calculated function value in the X register and a [RTN] instruction.
-
-
Specify Integration Limits:
-
In Run mode, enter the lower limit of integration (a), then press [ENTER], and enter the upper limit of integration (b).
-
-
Execute [f][∫]:
-
Press [f][∫] followed by the label of your function subroutine (e.g., [f][∫] A).
-
The calculator will iterate through calculations, sampling the function at various points within the integration interval and refining the approximation of the integral.
-
-
Interpret Results:
-
The approximate value of the integral will be displayed in the X register.
-
The Y register will contain an estimate of the uncertainty associated with the approximation.
-
4.4.3. Considerations for Accuracy
-
Display Format: The display format (fixed point, scientific, or engineering) influences the accuracy and speed of the integration. Generally, using more decimal places increases accuracy but also increases calculation time.
-
Function Behavior: Functions with rapid oscillations, discontinuities, or singularities within the integration interval may require special attention or alternative methods for accurate integration.
-
Uncertainty Estimate: The uncertainty value in the Y register provides an indication of the potential error in the approximation. If the uncertainty is too high for your needs, you may need to adjust the display format or consider alternative integration methods.
4.4.4. Applications of Numerical Integration
-
Calculating Areas: Find the area under a curve, representing physical quantities like work done or distance traveled.
-
Solving Differential Equations: Numerical integration is often used in conjunction with other numerical methods to solve differential equations that describe physical phenomena.
-
Probability and Statistics: Calculate probabilities and expected values for continuous random variables.
-
Engineering Applications: Evaluate complex engineering formulas and models involving integrals.
4.4.5. Additional Notes
-
Integration Limits: Ensure the integration limits are within the domain of the function and are entered in the correct order (lower limit first, then upper limit).
-
Subroutine Efficiency: Optimizing your function subroutine for speed and accuracy can improve the overall performance of numerical integration.
-
Alternative Methods: For complex functions or high accuracy requirements, consider exploring alternative numerical integration methods beyond the scope of this manual.
Numerical integration with the [f][∫] function expands the DM15’s capabilities, allowing you to tackle problems involving definite integrals that may be challenging to solve analytically. By understanding the principles and considerations involved, you can effectively utilize this powerful tool to find approximate solutions and gain insights into various mathematical and real-world problems.
5. Firmware
5.1. Firmware Update
| It is not possible to break or brick the calculator with any update procedure. |
| All calculator data (i.e. programs, registers, etc.) will be lost. Make a backup if needed. |
5.1.1. Selecting Firmware
5.1.1.1. The Latest Firmware
The latest firmware versions are available at https://technical.swissmicros.com/voyager/firmware/.
Download files using the 'Target save as…' function.
5.1.1.2. Name Conventions
The basic firmware name consist of two parts
<model>_<version>.hex Example: DM12_V31.hex
where
- <model>
-
Calculator model. One of
DM10,DM11,D12,DM15,DM16,DM41 - <version>
-
Firmware version, e.g.
V32.
Extended firmware name adds name of the extension
<model>_<ext>_<version>.hex Example: DM15_M80_V31.hex
where <model> and <version> are the same as above and
- <ext>
-
Name of the extension e.g.
M80,M1B
5.1.1.3. Special DM15 Firmware Versions
There are two special firmware versions for the DM15, version M80 and version M1B.
Both contain the original ROM with modifications to support more memory.
According to the HP-15C Owner’s Handbook, Appendix C: Memory Allocation (pg. 214), the
total allocatable memory is 64 registers and initial Memory Status is 19-46 0-0.
The following table summarizes how this limit is modified in extended DM15 ROMs.
| ROM | Alocatable registers | RAM base addr. | Initial Memory Status |
|---|---|---|---|
DM15 (Original ROM) |
64 |
0xc0 |
|
DM15_M80 |
128 |
0x80 |
|
DM15_M1B |
229 |
0x1b |
|
The default distribution version on DM15 is DM15_M1B with 229 Registers to supply
users with as much memory as possible. Please, keep in mind the original calculator
ROM isn’t designed to handle so much memory and there are known at least two marginal
cases when the calculator can give confusing info or wrong result:
|
Known problems
|
To avoid potential problems, the firmware version DM15_M80 can be used,
where such effects should be less prominent, or even firmware version DM15 with the original ROM code.
5.1.2. Update on Windows
5.1.2.1. Required software
-
Download and unpack the SwissMicros Voyage Firmware Tool for updating the calculator.
5.1.2.2. Update
-
Connect the calculator with a miniUSB cable to the computer.
-
Start the Voyage Firmware Tool
-
Press "Open File …" and choose the firmware file
-
Choose "Serial Port", see find Serial Port Number
-
Press the "Program" button in the application.
-
Press the reset button with a paperclip to initiate the flash process. If the calculator beeps and displays `SERIAL CONSOLE`, reset again until the flash process begins.
-
The flash progress is displayed in the application and takes about 10-20 seconds depending on the firmware version.
-
{post_flash ==== Update on MacOS
5.1.2.3. Required Software
-
Ensure the Serial Port driver is installed.
-
Download and install MacPort (www.macports.org)
-
Open the Terminal application (Applications→Utilities→Terminal) and run the following commands:
sudo port selfupdate sudo port upgrade outdated sudo port install lpc21isp
-
Close the Terminal application
5.1.2.4. Firmware Update
-
Open the Terminal application (Applications→Utilities→Terminal)
-
Connect the calculator with a miniUSB cable to the computer.
-
Run command:
sudo lpc21isp -control -controlinv -hex <firmware_file> <serial_port> 115200 12000
replace
<firmware_file>with the firmware file name
and<serial_port>with Serial Port Name found in previous stepExample:
sudo lpc21isp -control -controlinv -hex DM15_V31.hex /dev/tty.usbserial-0001 115200 12000
-
Press the reset button with a paperclip to initiate the flash process. If the calculator beeps and displays `SERIAL CONSOLE`, reset again until the flash process begins.
-
After the flash procedure is done, press the reset button again and disconnect from the computer.
-
Close the Terminal application
5.1.3. Update on Linux
5.1.3.1. Required Software
-
Install the
lpc21isptool for firmware update.On Debian based systems run
sudo apt-get install lpc21isp
or run package installer according to the Linux distribution.
5.1.3.2. Firmware Update
-
Start the flashing utility by
sudo lpc21isp <firmware_file> <serial_port> 115200 12000
replace
<firmware_file>with the appropriate firmware filename and<serial_port>with Serial Port Name found in the previous stepExample:
sudo lpc21isp DM15_V31.hex /dev/ttyUSB0 115200 12000
-
Wait for message "Synchronizing (ESC to abort)". Press the reset button with a paperclip to initiate the flash process. If the calculator beeps and displays `SERIAL CONSOLE`, reset again until the flash process begins.
-
After the flash procedure is done, press the reset button again and disconnect from the computer.
5.2. Serial Console
Useful links:
-
Encode and decode utility (html with jscript) for Save and Restore State function
-
A great HP-15C Simulator by Torsten Manz for Windows, Linux and Mac OS X supports data exchange with the DM15.
5.2.1. Connection to Serial Console
-
Prepare Serial Console program:
|
Remove the USB cable from the calculator if not needed.
Residual currents of the CP2102 chip can cause shortening of the battery life when left connected
for prolonged periods of time after the calculator is turned OFF. To be completely sure any residual charges are removed, turn the calculator ON/OFF after the USB cable is removed. |
5.2.2. Enable Serial Console Mode
Serial Console Mode is enabled by ON + C, see Special Key Combinations chapter for more details.
5.2.3. Serial Port Drivers
5.2.3.1. Windows
Download and install Silicon Labs CP2102 USB Driver from Silicon Labs drivers page/Downloads.
|
Windows users should NOT use the "Universal" Windows driver, use the older Windows drivers instead, the newer type has installation issues on Windows 10. |
5.2.3.2. MacOS
Driver is part of the system since "Big Sur".
For earlier systems download and install the CP2102 Mac OSX driver from Silicon Labs drivers page/Downloads.
5.2.3.3. Linux
No action needed.
The cp210x driver is part of the kernel build on all major Linux systems.
5.2.4. Finding Serial Port
5.2.4.1. Windows
-
Connect the calculator with a miniUSB cable to the computer.
-
Open Device Manager and find the
Silicon Labs CP210xline, -
Note the name given to the USB Serial Port (here :
COM3)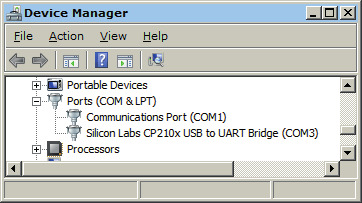
5.2.4.2. MacOS
-
Ensure the Serial Port driver is installed.
-
Connect the calculator with a miniUSB cable to the computer.
-
Find the name of the USB Serial Port
ls /dev/tty.usbserial*
or with Silicon Labs drivers
ls /dev/tty.SLAB*
The port is usually
/dev/tty.usbserial-0001or/dev/tty.SLAB_USBtoUART
If the port isn’t present, check the USB connection to calculator.
5.2.4.3. Linux
-
Connect the calculator with a miniUSB cable to the computer.
-
In the console run:
dmesg
There should be a message near the end like
cp210x converter now attached to ttyUSB0If so, the full path to the USB Serial Port is
/dev/ttyUSB0
5.2.5. Console on Windows
5.2.5.1. Required Software
Setting up a USB Serial Port connection in Windows
-
Download and install PuTTY (http://www.putty.org/)
5.2.5.2. Connection
-
Connect the calculator with a miniUSB cable to the computer.
-
Enable the Serial Console Mode on the calculator: ON + C + see Special Key Combinations chapter for more details.
-
Start PuTTY, go to Session
[1]and select Serial in the panel on the right; go to Connection[2]→ Serial[3]and configure the serial line with the following values:-
Serial line to connect to : Serial Port Name found in previous step
-
Speed : 38400
-
Data bits : 8
-
Stop bits : 1
-
Parity : None
-
Flow control : XON/XOFF (or none)
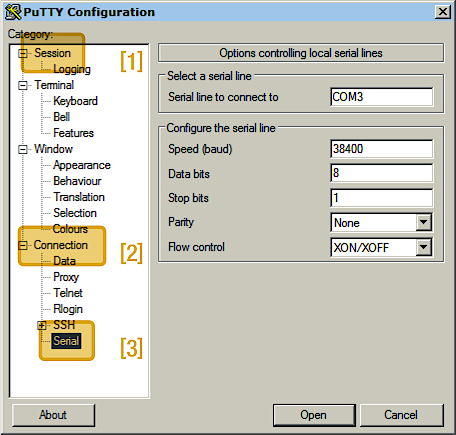
-
-
Click "Open" to start monitoring Serial Data.
-
The Serial Connection is now established. The monitor window is blank when it starts. Press «?» for help.
-
Pressing any button on the calculator ends the Serial Console Mode.
5.2.6. Console on MacOS
5.2.6.1. Required Software
-
Ensure the serial driver is installed.
-
The
screenutility is preinstalled on MacOS system.
5.2.6.2. Connection
-
Connect the calculator with a miniUSB cable to the computer.
-
Enable the Serial Console Mode on the calculator: ON + C + see Special Key Combinations chapter for more details.
-
Open the Terminal application (Applications→Utilities→Terminal)
-
Start a console session in terminal application:
screen <serial_port> 38400,8,n,1
replace
<serial_port>with serial port name found in previous stepExample:
screen /dev/tty.usbserial-0001 38400,8,n,1
-
The Serial Connection is now established. The monitor window is blank when it starts. Press «?» for help.
-
Pressing any button on the calculator ends the Serial Console Mode.
-
End the console session: press CONTROL + a then k then y
-
Disconnect the calculator
-
Close the Terminal application
5.2.7. Console on Linux
5.2.7.1. Required Software
-
Install the
putty.On Debian based systems run
sudo apt-get install putty
or run package installer according to the Linux distribution.
5.2.7.2. Connection
-
Connect the calculator with a miniUSB cable to the computer.
-
Start PuTTY
-
go to "Session" and select Serial in the panel on the right
-
go to Connection → Serial and configure the serial line using the following values. The rest should be left to default (check image below):
-
Serial line to connect to: use Serial Port Name found in the previous step
-
Speed : 38400
-
No flow control
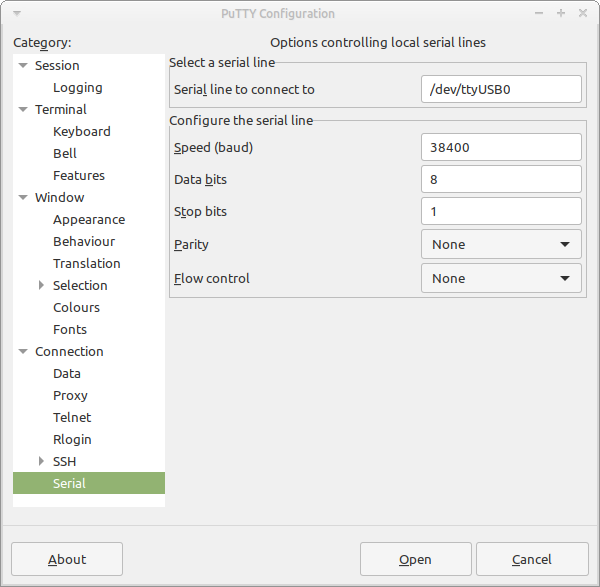
-
-
Enable the Serial Console Mode on the calculator: ON + C + see Special Key Combinations chapter for more details.
-
Click "Open" to start monitoring Serial Data.
-
The Serial Connection is now established. The monitor window is blank when it starts. Press «?» for help.
-
Pressing any button on the calculator ends the Serial Console Mode.
5.3. Commands in Serial Console
Once the serial connection to the calculator is established, calculator responds to switching to Serial Console Mode with text:
<model> ready
where <model> is calculator model, e.g. for DM15_M80 it writes to the serial console
DM15_M80 ready
This also indicates that the serial console is ready to accept commands.
As a response to ENTER in serial console window the calculator responds with
command prompt, which is
DM41>> - for DM41 model, or
VOYAGER >> - for other models
A command prompt is also displayed whenever the calculator finishes a command and is ready for the next one.
If an invalid command is entered or ? command is used, the calculator responds
with firmware version and list of available commands, e.g. for DM15_M80_V31:
VOYAGER >> ? Firmware DM15_M80_V32 ? Help p Key press s Dump memory l Load memory ct Console timeout bootloader Invoke Bootloader t Get time ts Set time td Update time kb Toggle keyboard output to console d Toggle display output to console b Read battery voltage Type '<command> ?' for params VOYAGER >>
Next chapters describe several important commands in more details.
5.3.1. Save and Restore State
Here state refers to the complete contents of the calculator, i.e. stack, registers, programs, etc.
Saving calculator memory
-
Establish a connection to the Serial Console
-
To dump contents of calculator memory, enter:
s -
The memory dump is displayed followed by command prompt
-
This dump can be copied, pasted and saved to a text file (including the short line at the top which describes the calculator model) to be later restored to the calculator
Restoring calculator memory
-
Establish a connection to the Serial Console
-
Engage calculator Restore Mode by entering:
l(lowercase «L») -
The command prompt changes to:
Waiting for data… -
Copy all characters from the memory dump, including the short line at the top which describes the calculator model
-
Paste it in the monitor window
-
Monitor window outputs:
Read OK
and the command prompt is displayed -
Calculator memory is now restored
5.3.2. Set time and date
Getting calculator internal date and time
-
Establish a connection to the Serial Console
-
In the serial monitor window, enter:
t -
The monitor window returns date, time and day of the week in format:
YYYY-MM-DD HH:MM:SS DDD
Setting date and time
-
Establish a connection to the Serial Console
-
The command to set date and time is
ts <YYYYMMDD> <HHMMSS>for instance for September 22nd of 2016, 6:30 PM, enter the following command:
ts 20160922 183000 -
Now, date and time are set
5.4. Calculator configuration
Configuration parameters can be directly changed by using special key combinations. Because the different models of the Voyager Series have different button layouts and almost, but not quite, similar configuration possibilities, in this chapter keys are referenced by their row/column place, e.g. (2-3) means the key in row 2 and column 3.
See Special Key Combinations for more details of how to invoke this function on a particular calculator model.
5.4.1. CPU Speed
Invocation: ON + (1-9)
The calculator supports two CPU speeds:
-
Normal - CPU runs at 12MHz
-
Fast - CPU runs at 48MHz
This key combination cycles through them.
5.4.2. LCD Contrast Configuration
Invocation: ON + (1-6)
This key combination starts LCD contrast configuration.
LCD contrast configuration consists of two parameters:
-
param1: LCD brightness
-
param2: LCD voltage
The LCD configuration:
-
is automatically left without any change after 10 seconds of inactivity.
-
can be left without configuration change at any time by ON key
-
current configuration can be confirmed and saved by ENTER key
5.4.3. LCD Contrast Reset
Invocation: ON + (2-6)
This key combination resets the LCD contrast configuration to the default values.
5.4.4. Fonts
Invocation: ON + (1-7)
This key combination cycles through the available font types.
5.4.5. Annunciator Location
Invocation: ON + (2-2)
This key combination toggles between location for the annunciators of the Voyager Series*, displayed either below the digits (default) or above the digits.
*except DM41
5.5. Special Key Combinations
The SwissMicros Voyager calculators have some special key combinations, some are the same as on the HP calculators, some are unique to SwissMicros calculators.
Usage:
-
Turn off calculator
-
Press and hold one of the buttons listed below
-
Press and release ON button
-
Release first button pressed
5.5.1. DM15
| Key | Function description |
|---|---|
A |
Display time/date for 5 minutes |
B |
Benchmark. Evaluate speed compared to original calculator |
C |
Switch to serial console (see Serial Console for details) |
E |
System info. Firmware version, battery voltage, current frequency, etc. |
CHS |
Change LCD contrast. Param1: up +, down −, Param2: up Σ+, down 3 |
EEX |
Reset LCD contrast to default values. |
STO |
Adjust RTC: decrement -1h |
RCL |
Adjust RTC: increment +1h |
7 |
|
9 |
Configure CPU speed. Toggle between 12MHz and 48MHz |
÷ |
Keyboard self test |
⨯ |
Self test |
− |
Power reset |
+ |
Endless test |
. |
Toggle decimal delimiter |
SST |
Time/date adjustment. |
GTO |
6. Appendices
6.1. Error Conditions
This appendix provides a comprehensive list of error messages that you may encounter while operating the DM15 calculator, along with their explanations and potential solutions. Understanding these error codes will help you troubleshoot any issues and ensure smooth calculations.
6.1.1. Error Codes and Explanations
-
Error 0: Improper Math Operation: This error occurs when you attempt a mathematically invalid operation, such as:
-
Division by zero
-
Taking the square root of a negative number (outside of Complex mode)
-
Raising a negative number to a non-integer power (outside of Complex mode)
-
Calculating the logarithm of a non-positive number
-
Other invalid mathematical operations depending on the function and mode
-
-
Error 1: Improper Matrix Operation: This error indicates an attempt to use a non-matrix function on a matrix or an incompatible matrix operation, such as:
-
Adding or subtracting matrices with incompatible dimensions
-
Multiplying matrices with incompatible dimensions
-
Inverting a non-square matrix
-
-
Error 2: Improper Statistics Operation: This error occurs when attempting a statistical calculation with insufficient or invalid data:
-
Calculating statistics with zero data points
-
Performing calculations requiring more than one data point with only one data point
-
Encountering division by zero or other invalid operations during statistical calculations
-
-
Error 3: Improper Register Number or Matrix Element: This error indicates an attempt to access a non-existent register or matrix element, such as:
-
Recalling or storing data in a register beyond the allocated memory range
-
Accessing a matrix element outside the defined dimensions of the matrix
-
-
Error 4: Improper Line Number or Label Call: This error occurs during programming when:
-
A line number referenced in a [GTO] instruction does not exist or is beyond the program memory range.
-
A label used in a [GTO] or [LBL] instruction does not exist.
-
There is insufficient memory to add a new program line.
-
-
Error 5: Subroutine Level Too Deep: This error indicates that you have exceeded the maximum nesting level of subroutines (7 levels deep).
-
Error 6: Improper Flag Number: This error occurs when attempting to access a flag number outside the valid range (0-9).
-
Error 7: Recursive [f][SOLVE] or [f][∫]: This error occurs when a subroutine called by [f][SOLVE] or [f][∫] attempts to use the same function within itself, creating a recursive loop.
-
Error 8: No Root Found: This error indicates that the [f][SOLVE] function could not find a root of the equation within the specified range or encountered a condition that prevented further refinement.
-
Error 10: Insufficient Memory: This error occurs when there is not enough available memory to perform the requested operation, such as dimensioning a large matrix or executing a complex program.
-
Error 11: Improper Matrix Argument: This error indicates that the arguments provided for a matrix operation are incompatible, such as using matrices with incorrect dimensions or attempting an invalid operation.
6.1.2. Troubleshooting Tips
-
Review Calculations: Carefully check your input values and the sequence of operations to ensure they are mathematically valid.
-
Check Memory Status: Use the [g][R←P] and [g][P←R] functions or the memory status display to verify that you have sufficient memory allocated for the desired operation.
-
Verify Program Logic: If an error occurs during program execution, use single-stepping or carefully review your program code to identify any logical errors or incorrect instructions.
-
Consult Manual: Refer to the relevant sections of this manual for detailed explanations of functions and operations to ensure you are using them correctly.
By understanding these error messages and their causes, you can effectively troubleshoot any issues encountered while using the DM15 and ensure accurate and efficient calculations. Remember, the calculator is designed to assist you in solving problems, and by understanding its feedback, you can maximize your productivity and avoid potential pitfalls.
6.2. Stack Diagrams
This appendix provides visual representations of the memory stack and its behavior during various operations on the DM15 calculator. These diagrams will help you understand how the stack interacts with different functions and how data moves within the stack registers.
6.2.1. Stack Representation
The memory stack of the DM15 consists of four registers, labelled T, Z, Y, and X, organized as follows:
T: (Top of Stack)
Z:
Y:
X: (Displayed Register)
-
The X register is at the bottom of the stack and always displayed on the screen.
-
The T register is at the top of the stack.
6.2.2. Stack Operations
6.2.2.1. Stack Lift
-
[ENTER]: This operation duplicates the value in the X register and pushes it up into the Y register. The stack lifts, and the previous contents of Y and Z registers move up to Z and T, respectively.
Before [ENTER]: (T: -, Z: -, Y: -, X: a)
After [ENTER]: (T: -, Z: -, Y: a, X: a)
-
Entering a Number: When you enter a number, it goes into the X register, causing the stack to lift.
Before: (T: c, Z: b, Y: a, X: -)
After: (T: b, Z: a, Y: c, X: new number)
6.2.2.2. Stack Drop
-
Two-Number Functions (e.g., [+], [-], [×], [÷]): These functions use the values in the X and Y registers, perform the operation, and store the result in the X register. The stack drops, and the contents of the Z and T registers move down to Y and Z, respectively.
Before: (T: c, Z: b, Y: a, X: x)
After: (T: c, Z: a, Y: result, X: result)
6.2.2.3. Roll Down ([R↓])
-
[R↓]: This function shifts the stack contents down one register. The value in X moves to T, the value in Y moves to X, and so on.
Before: (T: d, Z: c, Y: b, X: a)
After: (T: a, Z: d, Y: c, X: b)
6.2.2.4. Roll Up ([R↑])
-
[R↑]: This function shifts the stack contents up one register. The value in T moves to X, the value in Z moves to T, and so on.
Before: (T: d, Z: c, Y: b, X: a)
After: (T: c, Z: b, X: a, Y: d)
6.2.2.5. Exchange X and Y ([x↔y])
-
[x↔y]: This function swaps the values in the X and Y registers without affecting the rest of the stack.
Before: (T: c, Z: b, Y: a, X: x)
After: (T: c, Z: b, Y: x, X: a)
6.2.3. Stack Diagrams for Specific Functions
-
[g][LASTx]: Recalls the value from the LASTx register to the X register without affecting the stack.
-
[CLx]: Clears the X register to zero without affecting the other stack registers.
-
[g][Σ+] and [g][Σ-]: These functions, used for statistical calculations, do not affect the visible stack but operate on dedicated statistics registers.
6.2.4. Complex Mode Stack
In Complex mode, the DM15 uses two parallel stacks: one for the real parts and one for the imaginary parts of complex numbers. The stack operations behave similarly for both stacks, ensuring consistent and intuitive calculations with complex numbers.
6.2.5. Understanding Stack Behavior
By visualizing the stack and its operations, you can gain a deeper understanding of how the DM15 processes calculations. This knowledge is especially valuable for programming and debugging, as it allows you to track the movement of data and ensure your programs function as intended.
6.3. Memory Allocation and Management
This appendix delves into the memory structure of the DM15 calculator and how you can manage the allocation of memory between data storage and program instructions. Understanding memory management allows you to optimize the calculator’s resources for your specific needs.
6.3.1. Memory Structure
The DM15’s memory consists of 99 registers, each with a capacity of 7 bytes. These registers are divided into two main pools:
-
Data Storage Pool: This pool contains registers dedicated to storing numerical values and statistical data. It initially includes registers R0 through R19 (21 registers in total) but can be adjusted using memory management functions.
-
Common Pool: This pool contains registers available for various purposes, including:
-
Program Memory: Stores program instructions.
-
Matrix Memory: Stores matrix elements.
-
Complex Mode Stack: Stores the imaginary parts of complex numbers when Complex mode is active.
-
Advanced Functions: Provides temporary storage for advanced functions like [f][SOLVE] and [f][∫].
-
Uncommitted Registers: Registers not currently allocated to any specific use.
-
6.3.2. Memory Allocation
Initially, the DM15 allocates memory as follows:
-
Data Storage Pool: R0 - R19 (21 registers)
-
Common Pool: R20 - R97 (78 registers)
Within the common pool, registers are dynamically allocated as needed for program instructions, matrix elements, and advanced functions.
6.3.3. Memory Management Functions
-
[g][P←R]: This function converts registers from the common pool to the data storage pool, increasing the number of available data registers. Enter the desired number of data registers (1-97), then press [g][P←R].
-
[g][R←P]: This function converts registers from the data storage pool to the common pool, increasing the available memory for programs and advanced functions. Enter the desired number of data registers (1-97), then press [g][R←P].
Note:
-
Registers R0, R1, and I (Index register) are always part of the data storage pool and cannot be reallocated.
-
Reallocating registers may result in the loss of data stored in those registers, so exercise caution and back up important data before making changes.
-
The total number of registers remains constant at 99; only the distribution between the two pools changes.
6.3.4. Memory Usage
-
Program Memory: Most program instructions use 1 byte of memory, while some instructions, such as those involving labels or indirect addressing, may require 2 bytes. Refer to the programming section for a list of 2-byte instructions.
-
Matrix Memory: Each matrix element uses 1 register (7 bytes).
-
Complex Mode Stack: Activating Complex mode allocates 5 registers for the imaginary stack.
-
Advanced Functions: The [f][SOLVE] and [f][∫] functions require a temporary allocation of 5 and 23 registers, respectively.
6.3.5. Memory Status
-
Memory Status Display: Press and hold [g][R←P] to view the current memory allocation status. The display will show four numbers:
-
dd: Number of the highest data storage register (total data registers = dd + 2).
-
uu: Number of uncommitted registers in the common pool.
-
pp: Number of registers used for program memory.
-
b: Number of bytes remaining before another register is allocated to program memory.
-
-
[RCL] [g][P←R]: Recalls the current number of data storage registers (dd) to the X register.
6.3.6. Optimizing Memory Usage
-
Plan your programs: Before writing a program, estimate the number of instructions and required data storage to ensure sufficient memory is available.
-
Use subroutines: Subroutines promote code reuse and reduce program size, saving valuable memory space.
-
Optimize calculations: Explore alternative calculation methods that may require fewer steps or less memory.
-
Clear unnecessary data: Regularly clear data storage registers and matrices that are no longer needed to free up memory.
By effectively managing memory allocation, you can optimize the DM15’s resources for your specific needs, allowing you to create more complex programs, work with larger matrices, and leverage the full potential of this powerful calculator.
6.4. Advanced Use of [f][SOLVE]
This appendix provides deeper insights into the [f][SOLVE] function on the DM15 calculator, covering its underlying algorithm, advanced techniques for finding roots, and considerations for accuracy and efficiency.
6.4.1. Understanding the [f][SOLVE] Algorithm
The [f][SOLVE] function employs an iterative numerical method, specifically the secant method, to approximate the roots of equations. This method works by repeatedly refining an estimate of the root based on the function’s values at two previous estimates. Here’s a simplified overview of the process:
-
Initial Guesses: The algorithm starts with two initial guesses for the root, provided by the user.
-
Secant Line: A straight line (secant line) is drawn through the points corresponding to the function’s values at the two initial guesses.
-
New Estimate: The point where the secant line intersects the x-axis is taken as the new estimate for the root.
-
Iteration: The function is evaluated at the new estimate, and the process is repeated using the two most recent estimates, gradually refining the approximation of the root.
-
Termination: The algorithm terminates when one of the following conditions is met:
-
Convergence: The difference between successive estimates falls below a certain tolerance level, indicating that the approximation has converged to the root.
-
Maximum Iterations: A predefined maximum number of iterations is reached.
-
Error Condition: An error occurs during the calculation, such as division by zero or exceeding the calculator’s numerical limits.
-
6.4.2. Advanced Techniques for Finding Roots
-
Bracketing the Root: Providing initial guesses that bracket the root (one guess below and one above) significantly increases the likelihood of finding the root and improves convergence speed.
-
Multiple Roots: For equations with multiple roots, use different sets of initial guesses to locate each root.
-
Deflation: Once a root is found, you can modify the function subroutine to "deflate" it by dividing the original function by (x - root). This removes the found root from the equation, allowing you to search for other roots without the algorithm getting "stuck" at the known root.
-
Function Transformations: In some cases, transforming the equation or changing variables can simplify the function and make it easier to find roots.
6.4.3. Considerations for Accuracy and Efficiency
-
Initial Guesses: Choose initial guesses wisely to ensure convergence and avoid unnecessary iterations.
-
Function Behavior: Be aware of potential issues like discontinuities, singularities, or horizontal asymptotes that can affect the algorithm’s performance.
-
Numerical Precision: The calculator’s finite precision can introduce round-off errors, especially in complex calculations or with functions that have very steep slopes near the root.
-
Iteration Limit: The [f][SOLVE] function has a built-in limit on the number of iterations to prevent infinite loops. If the algorithm reaches this limit without converging, consider providing better initial guesses or exploring alternative methods.
6.4.4. Applications of Root Finding
-
Solving Equations: Find solutions to algebraic, transcendental, or implicit equations that are difficult or impossible to solve analytically.
-
Optimization Problems: Locate minimum or maximum values of functions by finding the roots of their derivatives.
-
Engineering Design: Determine critical parameters in engineering design problems, such as finding the dimensions of a structure that satisfies specific constraints.
-
Scientific Modeling: Analyze and interpret scientific models by finding the values of variables that satisfy the model’s equations.
By understanding the intricacies of the [f][SOLVE] function and its underlying algorithm, you can effectively utilize this powerful tool to tackle a wide range of problems that involve finding roots of equations. Remember, the success of root finding often relies on thoughtful analysis, careful selection of initial guesses, and awareness of the function’s behavior. With practice and exploration, you can unlock the full potential of [f][SOLVE] and enhance your problem-solving capabilities using the DM15 calculator.
6.5. Advanced Use of [f][∫]
This appendix delves deeper into the numerical integration capabilities of the DM15 calculator’s [f][∫] function. It explores the underlying algorithm, factors influencing accuracy and efficiency, and advanced techniques for handling complex integration problems.
6.5.1. Understanding the [f][∫] Algorithm
The [f][∫] function utilizes an adaptive quadrature method, specifically Gaussian quadrature, to approximate the definite integral of a function. This method works by dividing the integration interval into subintervals and applying a weighted sum of function values at specific points within each subinterval. Here’s a simplified overview:
-
Initial Subintervals: The algorithm starts by dividing the integration interval [a, b] into a small number of subintervals.
-
Gaussian Quadrature: Within each subinterval, the function is evaluated at specific points determined by Gaussian quadrature rules, and these values are weighted and summed to approximate the integral over that subinterval.
-
Error Estimation: The algorithm estimates the error associated with each subinterval’s approximation.
-
Adaptive Refinement: Subintervals with higher estimated errors are further subdivided, and the integration process is repeated on the smaller subintervals. This adaptive refinement focuses computational effort on regions where the function is more complex or changes rapidly.
-
Termination: The algorithm terminates when one of the following conditions is met:
-
Accuracy Goal: The overall estimated error falls below a certain tolerance level, typically determined by the display format and the desired accuracy.
-
Maximum Subdivisions: A predefined maximum number of subdivisions is reached.
-
Error Condition: An error occurs during the calculation, such as division by zero or exceeding the calculator’s numerical limits.
-
6.5.2. Factors Influencing Accuracy and Efficiency
-
Function Behavior: The complexity and smoothness of the function significantly impact the accuracy and efficiency of integration. Functions with rapid oscillations, discontinuities, or singularities may require more subdivisions and careful handling.
-
Integration Interval: The width of the integration interval can affect the number of subdivisions needed. Narrow intervals generally require fewer subdivisions, while wider intervals may need more to achieve the desired accuracy.
-
Display Format: The display format (fixed point, scientific, or engineering) determines the precision of the calculated function values and influences the overall accuracy of the integral approximation.
-
Subroutine Efficiency: The efficiency of your function subroutine can impact the overall calculation time. Optimizing your subroutine for speed and accuracy is crucial for efficient integration, especially for complex functions or large integration intervals.
6.5.3. Advanced Techniques
-
Subinterval Integration: For functions with known problematic regions (e.g., discontinuities), you can manually subdivide the integration interval and apply [f][∫] to each subinterval separately, then sum the results.
-
Change of Variables: In some cases, a change of variables can simplify the integrand or transform the integration interval, making the integral easier to compute numerically.
-
Alternative Methods: For highly oscillatory functions or integrals with singularities, explore specialized numerical integration methods beyond Gaussian quadrature.
6.5.4. Applications of Numerical Integration
-
Areas and Volumes: Calculate areas under curves, representing physical quantities like work done or distance traveled, and volumes of irregular shapes.
-
Probability and Statistics: Compute probabilities and expected values for continuous random variables.
-
Physics and Engineering: Evaluate physical quantities and solve problems involving integrals in various fields like mechanics, electromagnetism, and thermodynamics.
-
Financial Mathematics: Calculate present and future values of cash flows and perform other financial calculations involving integrals.
6.5.5. Additional Considerations
-
Convergence Issues: Be aware of potential convergence problems with certain functions or integration intervals. If the algorithm fails to converge, try adjusting the initial subdivision strategy, using a different quadrature rule, or exploring alternative integration methods.
-
Error Estimation: The uncertainty estimate provided by [f][∫] is just an approximation, and the actual error may be higher or lower. Be cautious when interpreting results and consider the potential for error propagation in subsequent calculations.
By delving into the advanced aspects of [f][∫] and numerical integration, you can expand your understanding of this powerful tool and tackle more complex integration problems with confidence. Remember, careful analysis, consideration of the function’s behavior, and appropriate choice of techniques are crucial for achieving accurate and efficient results using the DM15 calculator.
6.6. Batteries, Self-Tests, and Regulatory Information
This appendix provides essential information regarding the DM15 calculator’s batteries, self-test procedures, and compliance with regulatory standards.
6.6.1. Batteries
-
Battery Type: The DM15 uses a non-rechargeable 3-volt CR2032 lithium batteries.
-
Battery Life: Battery life depends on usage patterns. Performing complex calculations, running programs, or using the backlight will consume more power and reduce battery life.
-
Low Battery Indication: When the battery symbol appears in the lower-left corner of the display, it’s time to replace the batteries. Replace both batteries simultaneously to ensure consistent performance.
-
Battery Replacement:
-
Turn off the calculator.
-
Locate the battery compartment on the back of the calculator.
-
Use a small screwdriver or coin to open the battery compartment cover.
-
Remove the old batteries and insert new CR2032 lithium batteries, ensuring the positive (+) side faces upwards.
-
Close the battery compartment cover securely.
-
Turn on the calculator. If "MEMORY CLEAR" is displayed, press any key to clear it.
-
-
Battery Safety Precautions:
-
Use only specified or equivalent battery types.
-
Do not mix old and new batteries or different battery types.
-
Do not expose batteries to excessive heat or fire.
-
Dispose of used batteries properly according to local regulations.
-
6.6.2. Self-Tests
The DM15 includes self-test procedures to verify the calculator’s functionality and identify any potential issues.
-
Accessing Self-Tests:
-
Turn off the calculator.
-
Press and hold both [g] and [ENTER] keys.
-
While holding [g] and [ENTER], press the [ON] key.
-
Release all keys.
-
-
Test Options:
-
LCD Test: Press [1] to test the LCD segments. All segments should light up. Press any key to cycle through different display patterns and return to the main test menu.
-
Checksum Test: Press [2] to perform a checksum test and view firmware information. Press any key to return to the main test menu.
-
Keyboard Test: Press [3] to initiate the keyboard test. Press each key on the keyboard at least once. The display will progressively turn off as you press keys. Once all keys have been pressed, press any key to return to the main test menu.
-
-
Exiting Self-Tests: Press [ON] to exit the self-test mode and turn off the calculator.
6.6.3. Regulatory Information
The DM15 calculator complies with various regulatory standards and directives, including:
-
CE Marking (European Union): This marking indicates compliance with relevant EU directives, such as the Low Voltage Directive, EMC Directive, and RoHS Directive.
-
FCC Part 15 (United States): This regulation ensures that the calculator does not emit harmful electromagnetic interference.
-
Other Regional Standards: The DM15 may also comply with additional regional safety and electromagnetic compatibility standards depending on the specific market.
Note: Refer to the product label or accompanying documentation for specific regulatory information and compliance details.
6.6.4. Additional Information
For further assistance or inquiries regarding the DM15 calculator, its features, or regulatory compliance, please refer to the manufacturer’s website or contact customer support.
6.7. Differences Between the DM15 and Other RPN Calculators
This appendix highlights some key differences between the DM15 and other RPN calculators, particularly its predecessors or similar models. Understanding these distinctions will help you transition smoothly to the DM15 and leverage its unique features effectively.
6.7.1. Keyboard Layout and Functions
-
Key Arrangement: While the DM15 retains the fundamental RPN layout with the ENTER key and stack manipulation keys, the arrangement of specific function keys may differ from other models. Familiarize yourself with the DM15’s keyboard layout to locate functions efficiently.
-
Function Availability: The DM15 may offer a different set of built-in functions compared to other RPN calculators. Explore the available functions and their corresponding key combinations to fully utilize the calculator’s capabilities.
-
Alternate Functions: The assignment of alternate functions (accessed using the [f] and [g] prefix keys) may vary between models. Pay attention to the labelling on the keys to identify the correct key combinations for specific functions.
6.7.2. Memory and Performance
-
Memory Capacity: The DM15 may have a different memory capacity for storing programs and data compared to other models. Check the memory status display or refer to the manual for details on memory allocation and management.
-
Processing Speed: Advancements in technology may result in varying processing speeds between different calculator models. The DM15 may offer faster or slower performance compared to older or newer RPN calculators.
6.7.3. Display and User Interface
-
Display Technology: Different RPN calculators may utilize various display technologies, such as LCD, LED, or e-paper displays, resulting in differences in contrast, viewing angles, and power consumption.
-
Display Format Options: The DM15 may offer different display format options or varying levels of precision compared to other models. Explore the available display settings to customize the output according to your preferences.
6.7.4. Programming Features
-
Programming Model: While the core principles of RPN programming remain consistent, specific programming features or instructions may differ between calculator models. Refer to the DM15’s programming section for details on available instructions and programming techniques.
-
Memory Management: The methods for allocating memory between data storage and program instructions may vary between models. Consult the DM15’s manual for instructions on memory management and optimization.
6.7.5. Compatibility and Interfacing
-
Program Compatibility: Programs written for one RPN calculator model may not be directly compatible with another model due to differences in functions, instructions, or memory organization.
-
Data Transfer: The availability and methods for transferring data between the calculator and external devices or computers may vary between models.
6.7.6. Adapting to the DM15
-
Review the Manual: Carefully read the DM15’s user manual to familiarize yourself with its specific features, functions, and operating procedures.
-
Practice and Experiment: Spend time exploring the calculator’s capabilities through practice examples and experimentation to gain proficiency and comfort with its operation.
-
Seek Resources: Utilize online forums, user groups, or other resources dedicated to RPN calculators to learn tips, tricks, and advanced techniques.
By understanding the key differences between the DM15 and other RPN calculators, you can adapt to its unique characteristics and leverage its capabilities effectively. Remember, each calculator model offers its own set of advantages and limitations, and choosing the right tool depends on your individual needs and preferences.
6.8. Known Limitations and Troubleshooting
This appendix addresses some known limitations of the DM15 calculator and provides troubleshooting tips to help you overcome potential challenges and ensure smooth operation.
6.8.1. Known Limitations
-
Numerical Precision: Like all calculators, the DM15 has a finite numerical precision, which can lead to round-off errors in certain calculations, particularly those involving very large or very small numbers, or iterative processes. Be mindful of potential rounding errors and consider the significance of results in the context of your specific problem.
-
Memory Constraints: The DM15 has a limited amount of memory for storing programs and data. If you encounter memory limitations, try optimizing your programs, utilizing subroutines effectively, or reallocating memory as needed.
-
Complex Functions and Operations: While the DM15 supports complex number calculations and matrix operations, it may have limitations on the size and complexity of these operations compared to more advanced mathematical software. Be aware of potential restrictions and consider alternative methods or tools if necessary.
-
Programmable Functions: Certain functions on the DM15 may not be programmable within user programs due to their nature or the limitations of the calculator’s architecture. Refer to the programming section for a list of non-programmable functions.
6.8.2. Troubleshooting Tips
-
Unexpected Results:
-
Review Input: Double-check your input values and ensure they are entered correctly, including signs, units, and decimal places.
-
Check Settings: Verify that the calculator is in the appropriate mode (e.g., degrees or radians for trigonometric functions) and that the display format is set correctly.
-
Examine Program Logic: If an error occurs during program execution, carefully review your program code for logical errors, typos, or incorrect use of instructions. Utilize single-stepping or debugging techniques to identify the source of the problem.
-
-
Error Messages:
-
Refer to Appendix A: Consult the list of error codes and explanations in Appendix A to understand the cause of the error and take corrective action.
-
Clear Error and Retry: In many cases, you can simply clear the error message by pressing any key and retry the calculation or operation.
-
-
Memory Issues:
-
Memory Status: Check the memory status display to verify the available memory and allocation between data storage and program instructions.
-
Reallocate Memory: Use the [g][P←R] and [g][R←P] functions to adjust the memory allocation as needed.
-
Optimize Programs: Consider ways to reduce the memory footprint of your programs by using subroutines, efficient algorithms, and clearing unnecessary data.
-
-
Performance Issues:
-
Simplify Calculations: Explore alternative methods or formulas that may be less computationally intensive.
-
Break Down Problems: Divide complex problems into smaller, more manageable steps to reduce the load on the calculator.
-
6.8.3. Additional Resources
-
User Manual: Refer to the DM15’s user manual for detailed information on functions, operations, and programming techniques.
-
Online Forums and Communities: Seek assistance and share knowledge with other DM15 users through online forums or communities dedicated to RPN calculators.
-
Manufacturer Support: Contact the manufacturer’s customer support for further assistance with troubleshooting or technical issues.
By being aware of the DM15’s limitations and utilizing these troubleshooting tips, you can overcome potential challenges and maximize the effectiveness of this powerful calculator. Remember, understanding the tool and its behavior is crucial for achieving accurate results and successfully tackling complex problems.
6.9. DM15 Function Summary
This summary provides a quick reference guide to the various functions and operations available on the DM15 calculator. Refer to the corresponding sections in the user manual for detailed explanations and examples.
6.9.1. Basic Operations and Keyboard Functions
-
[ON]: Power on/off, reset Continuous Memory, change digit separator settings
-
[ENTER]: Separate number entries, duplicate X register value, enable/disable stack lift
-
[CHS]: Change sign of displayed number or exponent
-
[EEX]: Enter exponent for scientific notation
-
[←]: Backspace/delete digit, clear display, delete program instruction
-
[CLx]: Clear X register (display)
-
[f][CLΣ]: Clear statistics registers and stack
-
[f][CLx]: Clear program memory or reset program counter, clear prefix key
-
[f][CL REG]: Clear data storage registers
-
[g][LASTx]: Recall last X register value
-
[x↔y]: Exchange X and Y registers, exchange X register with data storage register
-
[R↓]: Roll down stack contents
-
[R↑]: Roll up stack contents
-
[f][USER]: Activate/deactivate User mode (swap primary and [f]-shifted functions for A-E keys)
6.9.2. Numeric Functions
-
[g][π]: Enter pi (π)
-
[g][INTG]: Integer part of displayed number
-
[f][FRAC]: Fractional part of displayed number
-
[g][RND]: Round displayed number
-
[g][ABS]: Absolute value of displayed number
-
[1/x]: Reciprocal of displayed number
-
[f][x!]: Factorial or Gamma function
-
[√x]: Square root
-
[g][x²]: Square
-
[yˣ]: Power function
-
[g][%]: Percentage calculation
-
[g][∆%]: Percentage change
-
[g][→P]: Rectangular to polar coordinates conversion
-
[f][→R]: Polar to rectangular coordinates conversion
-
[g][LN]: Natural logarithm
-
[eˣ]: Natural antilogarithm
-
[g][LOG]: Common logarithm (base 10)
-
[10ˣ]: Common antilogarithm (base 10)
-
[f][SINH]: Hyperbolic sine
-
[g][ASINH]: Inverse hyperbolic sine
-
[f][COSH]: Hyperbolic cosine
-
[g][ACOSH]: Inverse hyperbolic cosine
-
[f][TANH]: Hyperbolic tangent
-
[g][ATANH]: Inverse hyperbolic tangent
6.9.3. Trigonometric Functions
-
[g][DEG]: Set degrees mode
-
[g][RAD]: Set radians mode
-
[g][GRAD]: Set grads mode
-
[SIN]: Sine
-
[g][ASIN]: Arcsine
-
[COS]: Cosine
-
[g][ACOS]: Arccosine
-
[TAN]: Tangent
-
[g][ATAN]: Arctangent
-
[f][→HMS]: Decimal to hours/minutes/seconds or degrees/minutes/seconds
-
[g][→DEG]: Hours/minutes/seconds or degrees/minutes/seconds to decimal
6.9.4. Statistical Functions
-
[f][nPr]: Permutations
-
[g][nCr]: Combinations
-
[f][RND]: Random number generation
-
[STO][f][RND]: Store random number seed
-
[RCL][f][RND]: Recall random number seed
-
[g][Σ+]: Accumulate statistics
-
[RCL] [g][Σ+]: Recall Σx and Σy
-
[g][Σ-]: Remove data from statistics
-
[g][$\bar{x}$]: Mean calculation
-
[g][σx]: Sample standard deviation
-
[f][L.R.]: Linear regression (y-intercept and slope)
-
[f][ŷ]: Linear estimation and correlation coefficient
6.9.5. Data Storage and Memory Management
-
[STO]: Store value in register
-
[RCL]: Recall value from register
-
[g][P←R]: Allocate registers to data storage
-
[g][R←P]: Allocate registers to common pool
6.9.6. Programming Functions
-
[PRGM]: Enter/exit program mode
-
[LBL]: Set program label
-
[GTO]: Unconditional branch
-
[GTO] nnn: Jump to line number (not programmable)
-
[f][PSE]: Pause program execution
-
[R/S]: Stop/start program execution
-
[RTN]: Return from subroutine, end program
-
[x=y]: Test for equality
-
[x≠y]: Test for inequality
-
[g][x?]y: Indirect comparison tests
-
[f][FLAG]: Set flag
-
[f][SF]: Clear flag
-
[f][FS?]: Test flag
-
[f][ISG]: Increment and skip if greater
-
[f][DSZ]: Decrement and skip if zero
-
[f][SOLVE]: Solve for root of equation
-
[f][∫]: Numerical integration
6.9.7. Matrix Functions
-
[f][DIM]: Dimension a matrix
-
[g][MATRIX]: Store/recall matrix elements
-
[f][FILL]: Fill matrix with a value
-
[f][IDENTITY]: Create identity matrix
6.9.8. Appendix Functions
-
Error Codes (Appendix A): Refer to Appendix A for explanations of various error codes and troubleshooting tips.
-
Stack Diagrams (Appendix B): Visualize stack behavior during different operations using the diagrams in Appendix B.
-
Memory Management (Appendix C): Learn about memory allocation and management techniques in Appendix C.
-
Advanced [f][SOLVE] (Appendix D): Explore advanced aspects of the [f][SOLVE] function in Appendix D.
-
Advanced [f][∫] (Appendix E): Delve deeper into numerical integration techniques in Appendix E.
-
Batteries and Self-Tests (Appendix F): Find information on battery replacement and self-test procedures in Appendix F.
This function summary provides a concise overview of the DM15’s capabilities. Always refer to the user manual for detailed instructions, examples, and important notes on specific functions and operations.
6.10. DM15 Programming Summary
This summary provides a quick reference guide to the programming functions and techniques available on the DM15 calculator. Refer to the corresponding sections in the user manual for detailed explanations and examples.
6.10.1. Programming Modes and Navigation
-
[PRGM]: Enter/exit program mode
-
[GTO] nnn: Jump to specific line number (not programmable)
-
[SST]: Single-step through program instructions (not programmable)
-
[BST]: Back step through program instructions (not programmable)
-
[←]: Delete current program instruction
6.10.2. Program Structure and Instructions
-
[LBL]: Define a label for a program or subroutine
-
Labels (A-E, 0-9, .0-.9): Used with [LBL] to name programs and subroutines and with [GTO] to call or branch to them
-
[RTN]: Return from subroutine, end program execution
-
[R/S]: Stop/start program execution, used for program pauses and user input
6.10.3. Data Entry and Storage
-
[STO]: Store X register value in data storage register
-
[RCL]: Recall value from data storage register to X register
-
[x↔y]: Exchange X register with data storage register
-
Storage Arithmetic ([STO] [+], [-], [×], [÷]): Perform arithmetic with stored value and update register
-
Recall Arithmetic ([RCL] [+], [-], [×], [÷]): Perform arithmetic with stored value and display result
6.10.4. Control Flow
-
[GTO]: Unconditional branch to a labelled line
-
[x=y]: Test for equality between X and Y registers
-
[x≠y]: Test for inequality between X and Y registers
-
[g][x?]y: Indirect comparison tests (e.g., x > 0, x < y)
-
"Do if True" Rule: Program execution flow based on conditional tests
6.10.5. Flags
-
[f][FLAG]: Set a flag (0-9)
-
[f][SF]: Clear a flag (0-9)
-
[f][FS?]: Test if a flag is set (true)
6.10.6. Loop Control
-
[f][ISG]: Increment register and skip next instruction if greater than test value
-
[f][DSZ]: Decrement register and skip next instruction if zero or negative
6.10.7. Index Register
-
[STO] I: Store value in Index register
-
[RCL] I: Recall value from Index register
-
Indirect Addressing ([STO] (i), [RCL] (i), [GTO] (i)): Access data storage registers or program labels indirectly using the Index register
6.10.8. Subroutines
-
[GTO] Label: Call a subroutine
-
Nested Subroutines: Call one subroutine from within another (up to 7 levels deep)
6.10.9. User Mode
-
[f][USER]: Activate/deactivate User mode to simplify program execution using A-E keys
6.10.10. Advanced Functions
-
[f][SOLVE]: Find the root of an equation using a user-defined function subroutine
-
[f][∫]: Perform numerical integration using a user-defined function subroutine
6.10.11. Memory Management
-
[g][P←R]: Allocate registers to data storage pool
-
[g][R←P]: Allocate registers to common pool
-
Memory Status Display ([g][R←P] hold): View current memory allocation
6.10.12. Programming Tips
-
Plan and Design: Outline your program’s logic and structure before coding.
-
Use Comments: Add comments to your code to improve readability and understanding.
-
Modularize with Subroutines: Break down complex tasks into smaller subroutines for better organization and reusability.
-
Test and Debug: Thoroughly test your programs with various inputs and use debugging techniques like single-stepping to identify and fix errors.
-
Optimize for Efficiency: Consider memory usage and processing speed when writing programs.
With these programming functions and techniques, you can leverage the DM15’s capabilities to automate calculations, solve complex problems, and explore advanced mathematical concepts. Remember to consult the user manual for detailed instructions and examples to fully utilize the power of programming on the DM15.
6.11. Battery Replacement
|
SwissMicros Voyager calculators are powered by a non-rechargeable CR2032 battery. The battery should last many years with normal use. Powering via USB is not supported. |
-
Turn calculator off; calculator data is preserved for about 30 seconds without battery
-
Unscrew all four back screws
-
Remove calculator’s back
-
Replace the battery
-
Put it back together, don’t tighten the screws too much
7. Illustrations
7.1. Horizontal unit size comparison
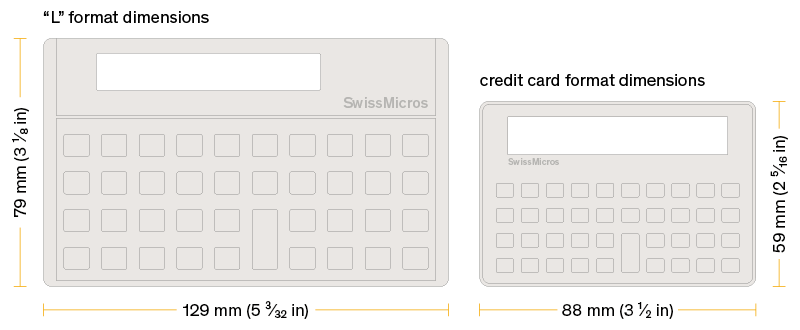
7.2. DM15L and DM15
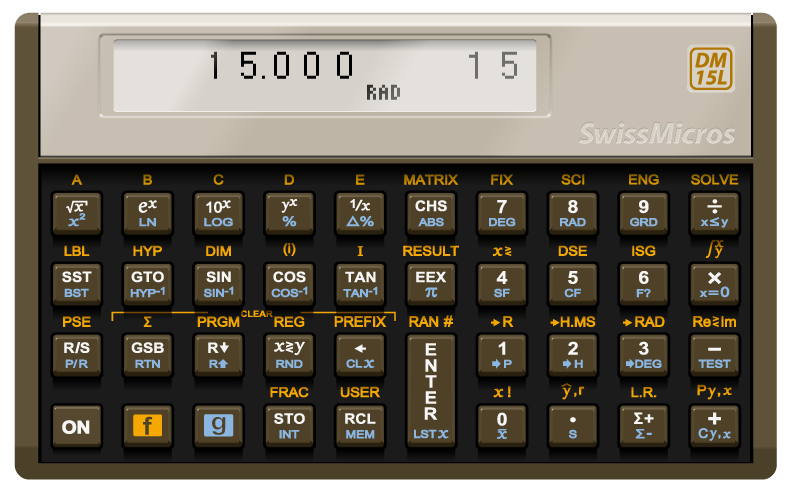

Appendix A: SDK
SwissMicros believes that the user should have full control over the hardware. SwissMicros provides an SDK to get developers started.
The Voyager Series SDK can be downloaded from: dm_lpc111x_sdk.tar.gz.
Appendix B: Matrices in Extended DM15
The hp15c was a highlight of its time. It is noteworthy that the original nut code of hp15c is apparently fit for an extension of its RAM. As far as I can say, it work best for all but the inverse of a matrix larger than 8x8. The largest matrix the original hp15c could store was 8x8 - so the algorithm was optimized for that maximum in size.
The reason why the original algorithm fail for larger matrices is that it has to reorder the rows of the matrix under certain circumstances. How the rows are reordered is stored in the signs of the diagonal elements of the matrix. In a register (7 bytes - 14 nibbles) the sign is stored in a nibble as 0 for + or 9 for -. A nibble hold 4 bits - so in the sign is place for additional 3 bits. These remaining 3 bits are used to store the original row offset. This only work up to 8 rows. If a matrix has more than 8 rows, this will not work anymore. :-(
The intermediate step used for matrix division, matrix inverse and determinant of a matrix is called LU decomposition. It is described in the "HP15C advanced functions handbook" - Section 4 - "Using Matrix Operations" - "Understanding the LU Decomposition" on page 96/97 of the original manual from 1982 or on page 82/83 of the reproduction from 2012.
Do not trust the results of matrix division, matrix inverse or determinant of a matrice larger than 8x8.
An easy counter-example:
A(i,j) = 0 if j < (n - i + 1); Otherwise A(i,j) = 1 b(i) = i 1 <= i,j <= n A*x = b ==> x(i) == 1 for all 1 <= i <= n ---- A * x = b 0 0 0 0 ... 0 1 x(1) = 1 0 0 0 0 ... 1 1 x(2) = 2 ... 0 1 1 1 ... 1 1 x(n-1) = n-1 1 1 1 1 ... 1 1 x(n) = n
The following program, also available as a dump, will fill pre-dimensioned matrix A, set size of b, fill b and set result matrix to C.
* f LBL D 001-42,21,14 RCL DIM A 002-45,23,11 STO 2 003- 44 2 g TEST 6 x≠y? 004-43,30, 6 g RTN 005- 43 32 f MATRIX 1 R0,R1 := 0 006-42,16, 1 * f LBL 0 007-42,21, 0 RCL 2 008- 45 2 RCL 0 009- 45 0 - 010- 30 1 011- 1 + 012- 40 RCL 1 013- 45 1 g TEST 8 x<y? 014-43,30, 8 g CLx 015- 43 45 g TEST 1 x>0? 016-43,30, 1 1 017- 1 USER STO A / USER 018u 44 11 GTO 0 019- 22 0 RCL 2 020- 45 2 1 021- 1 f DIM B 022-42,23,12 f MATRIX 1 R0,R1 := 0 023-42,16, 1 * f LBL 1 024-42,21, 1 RCL 0 025- 45 0 USER STO B / USER 026u 44 12 GTO 1 027- 22 1 f RESULT C 028-42,26,13 g RTN 029- 43 32
DM15_M1B 00 00000000000000 00000000000000 00000000000000 00b10000000000 04 000000fffff000 0000000000000c 00000000000008 c0b9ab9a000eae 08 00000000000000 2fafcbefbe2280 00000000000040 00000000000000 10 00000000000000 00000000000000 00000000000000 1a000000000000 14 01017980433000 1b2d2d2d2d2d2d 000000000005fb 00000000000000 18 00000000000000 0000000000007f 00000000c00000 00000000000000 bc 00000000000000 01000000000001 00000000000000 00000000000000 f8 00000000000000 00000000000000 00000000000000 0000b28c114bbf fc 300191ff9bf132 104abff171a278 31faf1fb303200 91ffb27642aa0d A: 000000fffff000 B: 000000fffffeae C: c0b9ab9a000eae M: f000bffffff7fb N: 00000000000000 G: 04
Then use it like this:
<n> ENTER f DIM A f D RCL MATRIX b RCL MATRIX A / f USER f MATRIX 1 RCL C RCL C ... f USER
To do the test:
-
Dimension A
-
Call D
-
Key in the calculation
-
Divide b by A
-
Check if all elements of C are equal to 1
If 0<n<9 all elements of C will be equal to 1, but if n>8 the algorithm will fail and C will hold totally wrong values. Due to an overflow, the display will blink.
Further investigations lead to the following results:
-
Mx 1x1 .. 8x8 give correct results.
-
Mx 9x9 .. 11x11 give wrong results.
-
Mx 12x12 .. 14x14 never end ⇒ endless loop